Alternative Method for Calculating Torque and Tension*

Lawrence Davis

53 Alternative Method for Calculating Torque and Tension*

If you would rather not think about finding lever arms, you can instead calculate the size of thetorque as the size of the force multiplied by the full distance to the pivot, and by the sine of the angle between the force and that full distance. Written in equation form it looks like this:

(1) $\begin{equation*} torque = \tau = F \cdot d \cdot sin\theta \end{equation*}$

Reinforcement Activity

The torque caused by a force depends on the angle between the line of action of the force acts and the line from where the force is applied to the pivot point. To feel this effect for yourself, try this:

Rotate a door by pushing at 90° to the door right at the outer edge.

Now apply the same force on the door, still on the very edge, but instead of pushing in a direction 90° to the door, push along the door, straight in toward the hinges. Does the door swing as it did before?

In the second case, the angle between the force direction and the distance to the pivot was 0° (they were parallel). Use the previous equation to show that the torque must be zero any time the line of action of the force goes straight through the rotation point (pivot).

Now, we know the force is 50 lbs, the distance from the pivot to the weight is 13.0 in length of the forearm and from the diagram we see the angle between the weight of the ball and the forearm distance is 60° (the same as the bicep-forearm angle because they are alternate interior angles). This is easier to see if we draw a stick figure diagram:

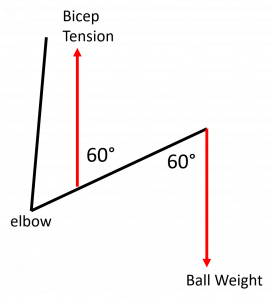
Stick diagram of a flexed arm holding a ball showing the bicep tension and weight and the angles between the forces and the forearm. Tension provided by the bicep is shown acting upward near the elbow and the weight of the ball acting downward on the weight. The acute (internal) angles between the forearm and each force are shown to be equivalent, in this case 60 degrees. — Stick diagram of a flexed arm holding a ball showing the bicep tension and weight and the angles between the forces and the forearm.

Now we can calculate the torque due to the ball weight $\tau_b$ as:

$\begin{equation*} \tau_b = F \cdot d \cdot sin\theta \end{equation*}$

$\begin{equation*} = 50\, \bold{lbs} \cdot 13\, \bold{in} \cdot sin(60\bold{\degree}) \end{equation*}$

$\begin{equation*} = 563\, \bold{in}\cdot\bold{lbs} \end{equation*}$

We have calculated the torque on the forearm due to the weight of the ball. You may be used to hearing about torque in $\bold{ft}\cdot\bold{lbs}$ rather than $\bold{in}\cdot\bold{lbs}$ , but we can always convert units later if we desire. For now, let’s keep working on finding the muscle tension.

We already know the torque due to the weight of the ball is $563\, \bold{in}\cdot\bold{lbs}$ so we just need to make sure that the tension in the biceps is large enough to cause the same torque even though it acts closer to the pivot. The biceps muscle torque, $\tau_{m}$ is:

$\begin{equation*} \tau_m = T \cdot d \cdot sin\theta \end{equation*}$

We just need to make this equal to the ball-weight-torque:

$\begin{equation*} T \cdot d \cdot sin\theta = 563\, \bold{in}\cdot\bold{lbs} \end{equation*}$

Then we divide both sides by $d$ and $sin\theta$ to isolate the bicep tension:

$\begin{equation*} T = \frac{563\, \bold{in}\cdot\bold{lbs}}{d \cdot sin\theta} \end{equation*}$

Finally we put in our values for $d$ and $\theta$ . Our original diagram gave us the distance as from bicep attachment to the pivot as 1.5 in and from our stick diagram we can see that the angle between the biceps tension and the distance is 180°-60° = 120°. We are ready to find the biceps tension value.

$\begin{equation*} T = \frac{563\, \cancel{\bold{in}}\cdot\bold{lbs}}{1.5\,\cancel{\bold{in}} \cdot sin(120\bold{\degree})} \end{equation*}$

$\begin{equation*} T = 433\,\bold{lbs} \end{equation*}$

Our result of 433 lbs seems surprisingly large, but we will see that forces even larger than this are common in the muscles, joints, and tendons of the body.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Reinforcement Activity

License

Share This Book