The method of hydrostatic weighing allows us to determine the average density () of an object without the need for a volume measurement, which can be difficult for large, odd objects like the human body. Instead, we measure only the object’s weight () and  apparent weight when submerged () and enter them into the equation below to calculate the density. To see how we arrive at this useful result, we first need to understand how the apparent weight is related to the buoyant force, and also how the buoyant force works.

(1)  

Apparent Weight

When an object is held still under water it appears to weigh less than it does in air because the buoyant force is helping to hold it up (balance its weight). For this reason, the reduced force you need to apply to hold the object is known as the apparent weight. When a scale is used to weigh an object submerged in water the scale will read the apparent weight. When performing hydrostatic weighing for body composition measurement the apparent weight is often called the under water weight ().

Static Equilibrium

When weighing under water we know the buoyant force must be equal to the difference in magnitude between the weight and apparent weight because the object remains still, which is a state known as static equilibrium. For an object to be in static equilibrium, all of the forces on it must be balanced so that there is no net force. For the case of under water weighing, the buoyant force plus the force provided by the scale must perfectly balance the weight of the object, as long as the object is holding still. We can use arrows to represent the forces on an object and visualize how they are balanced or unbalanced. This type of diagram is known as a free body diagram (FBD). The direction of arrows shows the direction of the forces and the arrow lengths shows the size (magnitude) of the force. In this case we call the arrows vectors and say the forces they represent are vector quantities.

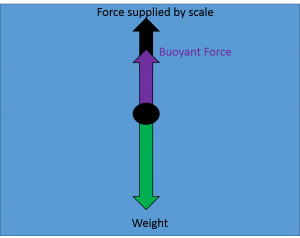
We learned in the last chapter that scales measure the force that they are supplying to other objects. When the buoyant force is also helping, the scale must supply less force to counteract the weight and maintain static equilibrium. Therefore the scale will provide a apparent weight reading that is less than the actual weight. As we see from the diagram above, the magnitudes of the force supplied by scale and buoyant force must balance the magnitude of the actual weight. In other words, we can calculate the buoyant force () as the difference between the magnitudes of weight () and apparent () weight read from the hanging scale.

Notice that if the object tended to float rather than sink, then the scale would need to pull downward to hold it in place. In that case the buoyant force would balance both the apparent force supplied by the scale and the actual weight so we could find the buoyant force as: