61 Preventing Injuries

Preventing Injuries

Injuries can be caused by large forces in the absence of any acceleration, such as static crushing injuries, and those types of injuries can be analyzed using concepts in Units 5 and 6. However,  injuries are more often caused by large forces associated with large accelerations.

Examples: Landing after a long fall

A person jumping from a height of 5 m, or about 20 ft, hits the ground with a speed of nearly 10 m/s, or about 22 mph (you can verify that using conservation of energy just as we did in the previous unit). Let’s calculate the average force applied to a 100 kg person after such a fall if the collision with the ground lasts 1/10 of a second. We start with Newton’s Second Law:

(1)   \begin{equation*} \bold{F_{ave}} = m \bold{a_{ave}} \end{equation*}

Remembering that direction is important when working with forces and accelerations, we need to define some directions. Let’s make downward negative so the initial velocity is -10 m/s. The final velocity is 0 m/s because the person comes to rest on the ground during landing. The stated collision duration was 0.1 s, so we are ready to calculate the average acceleration:

(2)   \begin{equation*} a_{ave}= \frac{\bold{\Delta v}}{\Delta t} =\frac{(0\,\bold{m/s})-10\,\bold{m/s})}{0.1\,\bold{s}} =100 \bold{m/s/s} \end{equation*}

    \begin{equation*} \bold{F_{ave}} = \frac{(100\,\bold{kg})(0\,\bold{m/s})-10\,\bold{m/s})}{0.1\,\bold{s}} = 10,000\,\bold{N} \end{equation*}

We see that the net force is positive, meaning that it points upward because we chose downward as the negative direction. This makes sense because the ground pushes up on the person to provide the impulse to stop the person’s downward motion.

Finally, we need to remember that we have calculated the average net force, which how much the forces are out of balance. This person has a weight of about 1,000 N  (100 kg x 9.8 m/s/s = 1000 N). Weight acts downward, so to get the required 10,000 N of net force upward there must actually be a 11,000 N applied upward on their feet, with 1000 N of that being cancelled out by their weight.

Spreading the force out over a longer time would reduce the average force (and peak force) applied to the person. For example, the the collision were made to last 5/10 of a second instead of 1/10 of a second, the acceleration would be five times smaller so the net force applied would also be five times smaller:

    \begin{equation*} \bold{F_{ave}} = \frac{(100\,\bold{kg})(0\,\bold{m/s})-(100\,\bold{kg})(-10\,\bold{m/s})}{0.5\,\bold{s}} = 5,000\,\bold{N} \end{equation*}

Adding the 1000 N body weight to get the total upward force on the body we get 6,000 N, or just 60% of the total when the collision lasted 0.1 s.

The people in the following video are well practiced at techniques for reducing forces by extending impact time.

Increasing the material strength of body tissues might would allow them to handle larger forces without injury and for certain body parts a regular exposure to forces that are not large enough to cause injury, also known as exercise, might increase tissue strength[1]. However, for many important body parts, such as the brain, the resistance to injury cannot be changed. That leaves us with three additional strategies for preventing injuries:

  1. Reduce the force applied to the body by decreasing the acceleration experienced by the body. Airbags work this way. The airbag increases the time over which the velocity of the head changes so that the acceleration is reduced, and thus the force is reduced.
  2. Ensure that forces are applied to stronger parts of the body. The headrest in your car works this way. The headrest ensures the forces required to move your head are applied to your skull instead of your neck.
  3. Increase the area of the body over which the force is applied to reduce the stress on each individual part. Climbing harnesses work this way. The harness spreads the total impact force applied to the climber over the hips, back, and legs so that no single body part experiences all of the force.

Everyday Example: Air Bags (Example of Strategy # 1)

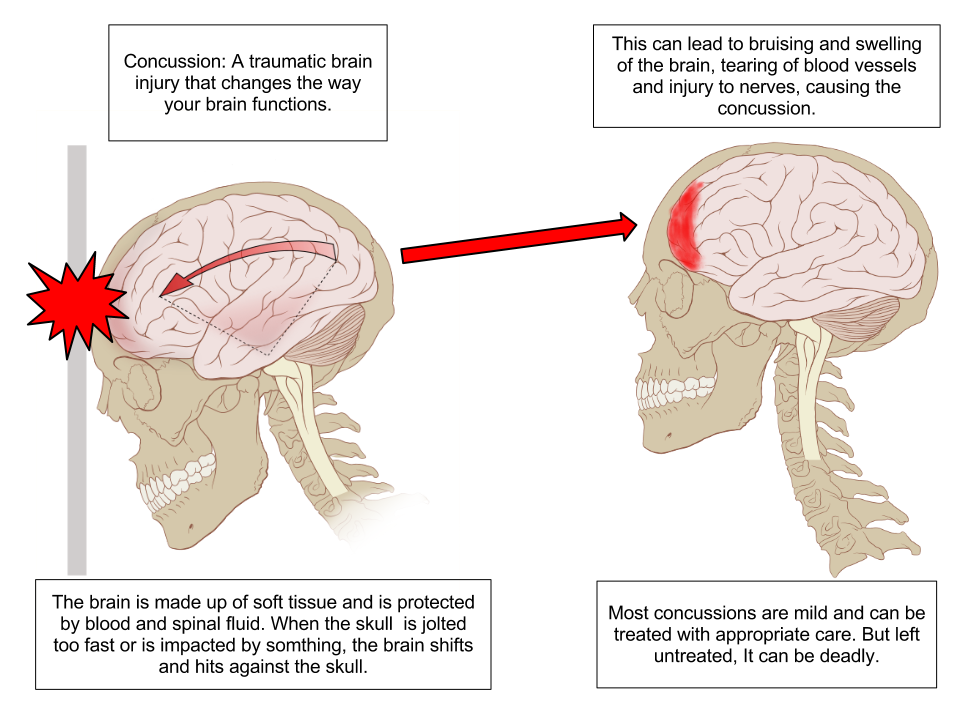First image: A human skull moving forward and stopping abruptly upon impact with a solid wall. A cutaway shows the brain continuing to move forward and impacting the front of the skull. Second image: The same skull with cutaway and injured area on the frontal lobe of the brain highlighted. Diagram of a concussion. “Concussion Anatomy” by Max Andrews via wikimedia commons.

[2]

When the head is travelling in a certain direction with constant speed the brain and skull are moving together. If an impact causes the the motion of the skull to change suddenly, then we know that the impact force must have been large (Newton’s Second Law). The skull may be able to handle the large force, but within the skull the brain has continued on with its original motion (Newton’s First Law) and it will eventually impact the skull and experience it’s own large acceleration and impact force. Recent research has shown that even without the occurrence of concussions, the damage caused by sub-concussive events like this can accumulate to cause Chronic Traumatic Encephalopathy (CTE)[3]. Airbags increase the time over which the head comes to rest, decreasing the acceleration of the head. The airbag also ensures that the head doesn’t bounce, which would cause the skull to be moving back into the brain, further increasing the impact force (more about how that works in the next unit).

Everyday Examples: Headrest (Example Strategy # 2)

First we need to recognize that the headrest in your car is not actually designed as a place to rest your head. The real purpose of the head rest is to minimize injury during a rear-end collision (like the one in the previous chapter). Applying Newton’s Laws can help us understand how they work.  When someone rear-ends your stationary car then it will accelerate forward. As a result your body is accelerated forward by normal force from the seat-back friction from the seat cushion. If the head rest were not there to push on your head, then in would tend to remain in place due to Newton's First Law, even as your body moved forward. That lag in head position gives the impression that the head snapped back, but really the body moved forward and left the head behind. Your head does actually remain attached to your accelerating body though, so the tissues in your neck must eventually provide the large force required to accelerate the head along with the body. According to Newton's Third Law, the tissues of the neck will feel an equal and opposite force to that which they apply to the head, as illustrated in the diagram below. That large force may damage the neck tissue (stress the tissue into it’s failure region).

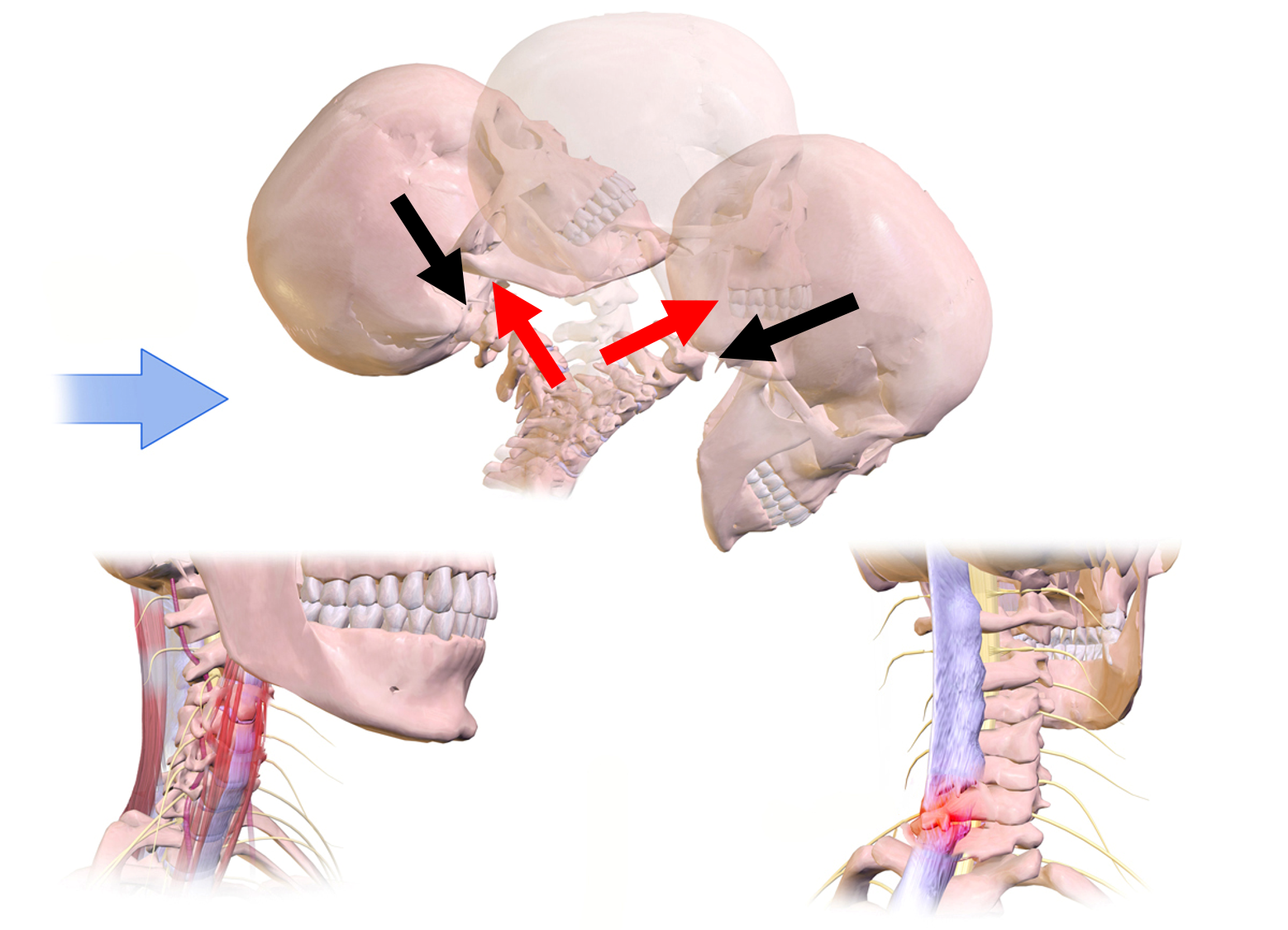
First image: The spine in a near vertical position while the head is moving from an extreme rearward position forward to a face-down position. Force pairs of equal length and opposite direction shown the force of the neck on the head and head back on the neck. Second and third images: Regions of injury on the front of the neck (soft tissue) and back of the neck (soft tissue and spine) are highlighted.
Top: Forces on the head from the neck (black) and on the neck from the head (red) during rapid forward-back motion of the head relative to the body. Bottom: Sites of whiplash injury. Image Credit: 3rd Law Whiplash is a derivative of Whiplash Injury by BruceBlaus, via Wikimedia Commons

[4]

With the headrest in place the head will accelerate along with the rest of your body.  Essentially the headrest applies a force to your head so that your neck doesn’t have to. In addition, the headrest is padded so that it compresses a bit, allowing your head to take slightly longer in getting up to speed than the car. That extra time reduces the acceleration of your head and so reduces the force applied by the headrest.

You can see the importance of the headrest in these crash-test videos:

Reinforcement Exercises

 

  1. Carlson, K. J., & Marchi, D. (2014). Reconstructing Mobility. New York: Springer. doi:10.1007/978-1-4899-7460-0 ↵
  2. Concussion Anatomy by Max Andrews - Own work. This file was derived from: Concussion mechanics.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=19490504 ↵
  3. "Concussion, microvascular injury, and early tauopathy in young athletes after impact head injury and an impact concussion mouse model" by Chad A Tagge, et. al, Brain, Oxford Academic ↵
  4. 3rd Law Whiplash is a derivative of Whiplash Injury by BruceBlaus [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)], via Wikimedia Commons ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Body Physics 2.0 Copyright © by Lawrence Davis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book