Exercise Answers: Module 30
Standard Deviation
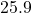 points
points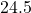 points
points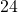 points (which occurred eight times)
points (which occurred eight times)- all three seem to represent the typical number of points scored; the mean is a bit high because there are no extremely low values but there are a few high values that pull the mean upwards.
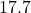 to
to 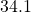 points
points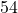 of the
of the 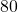 game results
game results- yes;
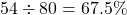
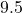 to
to 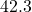 points
points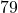 of the
of the 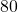 game results
game results- sort of close but not really;
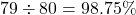
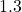 to
to 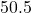 points
points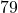 of the
of the 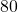 game results, again
game results, again- yes, this is pretty close;
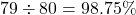
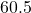 ;
; 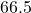
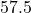 ;
; 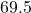
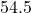 ;
; 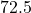
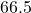 ;
; 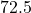
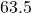 ;
; 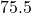
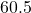 ;
; 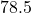
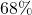 because
because 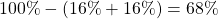
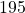 lb because this is halfway between
lb because this is halfway between 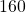 and
and 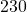 lb
lb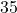 lb because
lb because  lb and
lb and 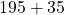 lb encompasses
lb encompasses 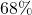 of the data
of the data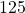 ;
; 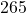
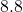 ;
; 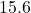
- You would not have predicted this from the data because it is more than two standard deviations below the mean, so there would be a roughly
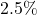 chance of this happening randomly. In fact,
chance of this happening randomly. In fact, 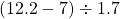 is slightly larger than
is slightly larger than 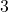 , so this is more than three standard deviations below the mean, making it even more unlikely. (You might have predicted that the Patriots would get worse when Tom Brady left them for Tampa Bay, but you wouldn’t have predicted only
, so this is more than three standard deviations below the mean, making it even more unlikely. (You might have predicted that the Patriots would get worse when Tom Brady left them for Tampa Bay, but you wouldn’t have predicted only 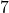 wins based on the previous nineteen years of data.)
wins based on the previous nineteen years of data.) 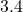 ;
; 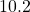
- You would not predict this from the data because it is more than two standard deviations above the mean, so there would be a roughly
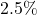 chance of this happening randomly. In fact,
chance of this happening randomly. In fact, 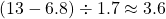 , so this is more than three standard deviations above the mean, making it even more unlikely. This increased win total is partly due to external forces (i.e., the Patriots becoming weaker and losing two games to the Bills) but even
, so this is more than three standard deviations above the mean, making it even more unlikely. This increased win total is partly due to external forces (i.e., the Patriots becoming weaker and losing two games to the Bills) but even  wins would have been a bold prediction, let alone
wins would have been a bold prediction, let alone 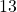 .
. 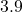 ;
; 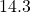
- The trouble with making predictions about the Broncos is that their standard deviation is so large. You could choose any number between
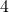 and
and 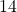 wins and be within the
wins and be within the 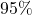 interval.
interval. 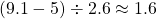 , so this is around
, so this is around 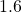 standard deviations below the mean, which makes it not very unusual. Whereas the Patriots and Bills are more consistent, the Broncos’ win totals fluctuate quite a bit and are therefore more unpredictable.
standard deviations below the mean, which makes it not very unusual. Whereas the Patriots and Bills are more consistent, the Broncos’ win totals fluctuate quite a bit and are therefore more unpredictable.

