Module 21: Converting Units of Area

Morgan Chase

Module 21: Converting Units of Area

You may use a calculator throughout this module.

Converting between units of area requires us to be careful because square units behave differently than linear units.

U.S. System: Converting Measurements of Area

a square that has sides 1 yard long

Consider a square yard; the area of a square with sides $1$ yard long.

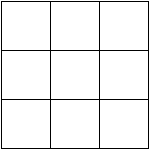
a 3 by 3 grid representing 9 square feet

$1$ yard = $3$ feet, so we can divide the square into three sections vertically and three sections horizontally to convert both dimensions of the square from yards to feet. This forms a $3$ by $3$ grid, which shows us visually that $1$ square yard equals $9$ square feet, not $3$ square feet! The linear conversion ratio of $1$ to $3$ means that that the conversion ratio for the areas is $1$ to $3^2$ , or $1$ to $9$ .

Here’s another way to think about it without a diagram: $1\text{ yd}=3\text{ ft}$ , so $(1\text{ yd})^2=(3\text{ ft})^2$ . To remove the parentheses, we must square the number and square the units: $(3\text{ ft})^2= 3^2\text{ ft}^2=9\text{ ft}^2$ .

More generally, we need to square the linear conversion factors when converting units of area. If the linear units have a ratio of $1$ to $n$ , the square units will have a ratio of $1$ to $n^2$ .

Exercises

1. An acre is defined as the area of a $660$ foot by $66$ foot rectangle. (That’s a furlong by a chain, if you were curious.) How many square feet are in $1$ acre?

2. How many square yards are in $1$ acre?

3. How many square inches equals $1$ square foot?

It should be no surprise that this module will be full of conversion ratios. As always, if you discover other conversion ratios that aren’t provided here, it would be a good idea to write them down so you can use them as needed.

$1\text{ ft}^2=144\text{ in}^2$

$1\text{ yd}^2=9\text{ ft}^2$

$1\text{ acre (ac)}=43,560\text{ ft}^2$

$1\text{ ac}=4,840\text{ yd}^2$

$1\text{ mi}^2=27,878,400\text{ ft}^2$

$1\text{ mi}^2=3,097,600\text{ yd}^2$

$1\text{ mi}^2=640\text{ ac}$

An acre is defined as a unit of area; it would be wrong to say “acres squared” or put an exponent of $2$ on the units.

Exercises

4. A hallway is $9$ yards long and $2$ yards wide. How many square feet of linoleum are needed to cover the hallway?

5. A proposed site for an elementary school is $600$ feet by $600$ feet. Find its area, in acres.

Metric System: Converting Measurements of Area

$1\text{ cm}^2=100\text{ mm}^2$

$1\text{ m}^2=1,000,000\text{ mm}^2$

$1\text{ m}^2=10,000\text{ cm}^2$

$1\text{ hectare (ha)}=10,000\text{ m}^2$

$1\text{ km}^2=1,000,000\text{ m}^2$

$1\text{ km}^2=100\text{ ha}$

A hectare is defined as a square with sides $100$ meters long. Dividing a square kilometer into ten rows and ten columns will make a $10$ by $10$ grid of $100$ hectares. As with acres, it would be wrong to say “hectares squared” or put an exponent of $2$ on the units.

Exercises

6. A hallway is $9$ meters long and $2$ meters wide. How many square centimeters of linoleum are needed to cover the hallway?

7. A proposed site for an elementary school is $200$ meters by $200$ meters. Find its area, in hectares.

Both Systems: Converting Measurements of Area

Converting between the U.S. and metric systems will involve messy decimal values. For example, because $1\text{ in}=2.54\text{ cm}$ , we can square both numbers and find that $(1\text{ in})^2=(2.54\text{ cm})^2=6.4516\text{ cm}^2$ . The conversions are rounded to three or four significant digits in the table below.

$1\text{ in}^2\approx6.45\text{ cm}^2\leftrightarrow1\text{ cm}^2\approx0.155\text{ in}^2$

$1\text{ yd}^2\approx0.836\text{ m}^2\leftrightarrow1\text{ m}^2\approx1.196\text{ yd}^2$

$1\text{ mi}^2\approx2.59\text{ km}^2\leftrightarrow1\text{ km}^2\approx0.386\text{ mi}^2$

$1\text{ ac}\approx0.405\text{ ha}\leftrightarrow1\text{ ha}\approx2.47\text{ ac}$

Exercises

8. The area of Portland is $145\text{ mi}^2$ . Convert this area to square kilometers.

9. How many hectares is a $5,000$ acre ranch?

10. A sheet of paper measures $8.5$ inches by $11$ inches. What is the area in square centimeters?

11. A soccer field is $100$ meters long and $70$ meters wide. What is its area in square feet?

Areas of Similar Figures

Earlier in this module, it was stated that if the linear units have a ratio of $1$ to $n$ , the square units will have a ratio of $1$ to $n^2$ . This applies to similar figures as well.

If the linear dimensions of two similar figures have a ratio of $1$ to $n$ , then the areas will have a ratio of $1$ to $n^2$ .

This is true for circles, similar triangles, similar rectangles, similar hexagons, you name it. We’ll verify this in the following exercises.

Exercises

A personal pizza has a $7$ -inch diameter. A medium pizza has a diameter twice that of a personal pizza.

12. Determine the area of the medium pizza.

13. Determine the area of the personal pizza.

14. What is the ratio of the areas of the two pizzas?

Right triangle $ABC$ has legs $3\text{ cm}$ and $4\text{ cm}$ long. Right triangle $DEF$ has legs triple the length of $ABC$ ’s.

15. Determine the area of the larger triangle, $DEF$ .

16. Determine the area of the smaller triangle, $ABC$ .

17. What is the ratio of the areas of the two triangles?

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License