Module 28: Mean, Median, Mode
You may use a calculator throughout this module.
We often describe data using a measure of central tendency. This is a number that we use to describe the typical data value. We will now look at the mean, the median, and the mode.
Mean
The mean of a set of data is what we commonly call the average: add up all of the numbers and then divide by how many numbers there were.
Exercises
1. The table below shows the average price of a gallon of regular unleaded gasoline in the Seattle metro area for ten weeks in Fall 2019. Compute the mean price over this time period.[1]
| Sep 16, 2019 | $ |
| Sep 23, 2019 | $ |
| Sep 30, 2019 | $ |
| Oct 07, 2019 | $ |
| Oct 14, 2019 | $ |
| Oct 21, 2019 | $ |
| Oct 28, 2019 | $ |
| Nov 04, 2019 | $ |
| Nov 11, 2019 | $ |
| Nov 18, 2019 | $ |
2. The table below shows the average price of a gallon of regular unleaded gasoline in the Seattle metro area for ten weeks in Fall 2008. Compute the mean price over this time period.[2]
| Sep 15, 2008 | $ |
| Sep 22, 2008 | $ |
| Sep 29, 2008 | $ |
| Oct 06, 2008 | $ |
| Oct 13, 2008 | $ |
| Oct 20, 2008 | $ |
| Oct 27, 2008 | $ |
| Nov 03, 2008 | $ |
| Nov 10, 2008 | $ |
| Nov 17, 2008 | $ |
Median
The median is the middle number in a set of data; it has an equal number of data values below it as above it. The numbers must be arranged in order, usually smallest to largest but largest to smallest would also work. Then we can count in from both ends of the list and find the median in the middle.
If there are an odd number of data values, there will be one number in the middle, which is the median.
If there are an even number of data values, there will be two numbers in the middle. The mean of these two numbers is the median.
Exercises
The houses on a block have these property values: $ ![]() ; $
; $ ![]() ; $
; $ ![]() ; $
; $ ![]() ; $
; $ ![]() .
.
3. Find the mean property value.
4. Find the median property value.
A new house is built on the block, making the property values $ ![]() ; $
; $ ![]() ; $
; $ ![]() ; $
; $ ![]() ; $
; $ ![]() and $
and $ ![]() .
.
5. Find the mean property value.
6. Find the median property value.
7. Which of these measures appears to give a more accurate representation of the typical house on the block?
The mean is better to work with when we do more complicated statistical analysis, but it is sensitive to extreme values; in other words, one very large or very small number can have a significant effect on the mean. The median is not sensitive to extreme values, which can make it a better measure to use when describing data that has one or two numbers very different from the remainder of the data.
For example, suppose you had ten quizzes, and you scored ![]() on nine of them but missed one quiz and received a score of
on nine of them but missed one quiz and received a score of ![]() . You earned a total of
. You earned a total of ![]() points over
points over ![]() quizzes, making your mean score
quizzes, making your mean score ![]() . However, your median score would be
. However, your median score would be ![]() because the median is calculated based on your fifth and sixth highest scores.
because the median is calculated based on your fifth and sixth highest scores.
Mode
In the example above, ![]() is also the mode of your scores because it is the most common quiz score in your gradebook. The mode is the value that appears most frequently in the data set. On the game show Family Feud, the goal is to guess the mode: the most popular answer.
is also the mode of your scores because it is the most common quiz score in your gradebook. The mode is the value that appears most frequently in the data set. On the game show Family Feud, the goal is to guess the mode: the most popular answer.
If no numbers are repeated, then the data set has no mode. If there are two values that are tied for most frequently occurring, then they are both considered a mode and the data set is called bimodal. If there are more than two values tied for the lead, we usually say that there is no mode.[3] (It’s like in sports: there is usually one MVP, but occasionally there are two co-MVPs. Having three or more MVPs would start to get ridiculous.)
Exercises
8. One hundred cell phone owners are asked which carrier they use. What is the mode of the data?
| AT&T Mobility | Verizon Wireless | T-Mobile US | Dish Wireless | U.S. Cellular |
9. Fifty people are asked what their favorite type of Girl Scout cookie is. What is the mode?
| S’Mores | Samoas | Tagalongs | Trefoils | Thin Mints |
Let’s put it all together and find the mean, median, and mode of some data sets. Sportsball!
From 2001-2019, these are the numbers of games won by the New England Patriots each NFL season.[4]
| year | wins |
| 2001 | |
| 2002 | |
| 2003 | |
| 2004 | |
| 2005 | |
| 2006 | |
| 2007 | |
| 2008 | |
| 2009 | |
| 2010 | |
| 2011 | |
| 2012 | |
| 2013 | |
| 2014 | |
| 2015 | |
| 2016 | |
| 2017 | |
| 2018 | |
| 2019 |
Exercises
10. Find the mean number of games won from 2001 to 2019.
11. Find the median number of games won from 2001 to 2019.
12. Find the mode of the number of games won from 2001 to 2019.
13. Do any of these measures appear to be misleading, or do they all represent the data fairly well?
From 2001-2019, these are the numbers of games won by the Buffalo Bills each NFL season.[5]
| year | wins |
| 2001 | |
| 2002 | |
| 2003 | |
| 2004 | |
| 2005 | |
| 2006 | |
| 2007 | |
| 2008 | |
| 2009 | |
| 2010 | |
| 2011 | |
| 2012 | |
| 2013 | |
| 2014 | |
| 2015 | |
| 2016 | |
| 2017 | |
| 2018 | |
| 2019 |
Exercises
14. Find the mean number of games won from 2001 to 2019.
15. Find the median number of games won from 2001 to 2019.
16. Find the mode of the number of games won from 2001 to 2019.
17. Do any of these measures appear to be misleading, or do they all represent the data fairly well?
Some sets of data may not be easy to describe with one measure of central tendency.
Exercises

Thirteen clementines are weighed. Their masses, in grams, are
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
18. Determine the mean. Does the mean appear to represent the mass of a typical clementine?
19. Determine the median. Does the median appear to represent the mass of a typical clementine?
20. Determine the mode. Does the mode appear to represent the mass of a typical clementine?
Suppose that the 108-gram clementine is a tiny bit heavier and the masses are actually
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
21. Determine the new mean. Is the new mean different from the original mean?
22. Determine the new median. Is the new median different from the original median?
23. Determine the new mode. Is the new mode different from the original mode? Does it represent the mass of a typical clementine?

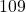 grams.
grams.- Source: https://www.eia.gov/petroleum/gasdiesel/ ↵
- Source: https://www.eia.gov/petroleum/gasdiesel/ ↵
- The concepts of trimodal and multimodal data exist, but we aren't going to consider anything beyond bimodal in this textbook. ↵
- Source: https://www.pro-football-reference.com/teams/nwe/index.htm ↵
- Source: https://www.pro-football-reference.com/teams/buf/index.htm ↵

