Module 26: Pyramids and Cones

You may use a calculator throughout this module.

Note: We will not necessarily follow the rules for rounding (precision and accuracy) in this module. Many of these figures have dimensions with only one significant figure, but we would lose a lot of information if we rounded the results to only one sig fig.

In the answer key, we will often round to the nearest whole number, or to the nearest tenth, or to two or three significant figures as we deem appropriate.

Pyramids

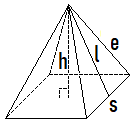
A pyramid is a geometric solid with a polygon base and triangular faces with a common vertex (called the apex of the pyramid). Pyramids are named according to the shape of their bases. The most common pyramids have a square or another regular polygon for a base, making all of the faces identical isosceles triangles. The height, h, is the distance from the apex straight down to the center of the base. Two other measures used with pyramids are the edge length e, the sides of the triangular faces, and the slant height l, the height of the triangular faces.

Volume of a Pyramid

In general, the volume of a pyramid with base of area B and height h is

V=\frac{1}{3}Bh or V=Bh\div3

If the base is a square with side length s, the volume is

V=\frac{1}{3}s^{2}h or V=s^{2}h\div3

Interestingly, the volume of a pyramid is \frac{1}{3} the volume of a prism with the same base and height.

Exercises

1. A pyramid has a square base with sides 16 centimeters long, and a height of 15 centimeters. Find the volume of the pyramid.

2. The Great Pyramid at Giza in Egypt has a height of 137 meters and a square base with sides 230 meters long.[1] Find the volume of the pyramid.

The lateral surface area (LSA) of a pyramid is found by adding the area of each triangular face.

Lateral Surface Area of a Pyramid

If the base of a pyramid is a regular polygon with n sides each of length s, and the slant height is l, then

LSA=\frac{1}{2}nsl or LSA=nsl\div2

If the base is a square, then

LSA=2sl

The total surface area (TSA) is of course found by adding the area of the base B to the lateral surface area. If the base is a regular polygon, you will need to use the techniques we studied in a previous module.

Total Surface Area of a Pyramid

TSA=LSA+B

If the base is a square, then

TSA=2sl+s^2

Exercises

3. A pyramid has a square base with sides 16 centimeters long, and a slant height of 17 centimeters. Find the lateral surface area and total surface area of the pyramid.

4. The Great Pyramid at Giza has a slant height of 179 meters and a square base with sides 230 meters long. Find the lateral surface area of the pyramid.

Cones

A cone is like a pyramid with a circular base.

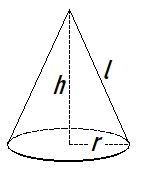
You may be able to determine the height h of a cone (the altitude from the apex, perpendicular to the base), or the slant height l (which is the length from the apex to the edge of the circular base). Note that the height, radius, and slant height form a right triangle with the slant height as the hypotenuse. We can use the Pythagorean theorem to determine the following equivalences.

The slant heightl, height h, and radius r of a cone are related as follows:

l=\sqrt{r^2+h^2}

h=\sqrt{l^2-r^2}

r=\sqrt{l^2-h^2}

Just as the volume of a pyramid is \frac{1}{3} the volume of a prism with the same base and height, the volume of a cone is \frac{1}{3} the volume of a cylinder with the same base and height.

Volume of a Cone

The volume of a cone with a base radius r and height h is

V=\frac{1}{3}\pi{r^2}h or V=\pi{r^2}h\div3

Exercises

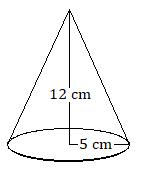
5. The base of a cone has a radius of 5 centimeters, and the vertical height of the cone is 12 centimeters. Find the volume of the cone.

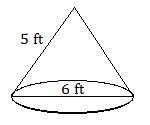
6. The base of a cone has a diameter of 6 feet, and the slant height of the cone is 5 feet. Find the volume of the cone.

For the surface area of a cone, we have the following formulas.

Surface Area of a Cone

LSA=\pi{rl}

TSA=LSA+\pi{r^2}=\pi{rl}+\pi{r^2}

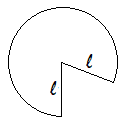
It’s hard to explain the justification for the LSA formula in words, but here goes. The lateral surface of a cone, when flattened out, is a circle with radius l that is missing a wedge. The circumference of this partial circle, because it matched the circumference of the circular base, is 2\pi{r}. The circumference of the entire circle with radius l would be 2\pi{l}, so the part we have is just a fraction of the entire circle. To be precise, the fraction is \frac{2\pi{r}}{2\pi{l}}, which reduces to \frac{r}{l}. The area of the entire circle with radius l would be \pi{l^2}. Because the partial circle is the fraction \frac{r}{l} of the entire circle, the area of the partial circle is \pi{l^2}\cdot\frac{r}{l}=\pi{rl}.

Exercises

7. The base of a cone has a diameter of 6 feet, and the slant height of the cone is 5 feet. Find the lateral surface area and total surface area of the cone.

8. The base of a cone has a radius of 5 centimeters, and the vertical height of the cone is 12 centimeters. Find the lateral surface area and total surface area of the cone.

Now that we have looked at the five major solids—prism, cylinder, sphere, pyramid, cone—you should be able to handle composite solids made from these shapes. Just remember to take them in pieces.

Exercises

A 250-gallon propane tank is roughly in the shape of a cylinder with a hemisphere on each end. The length of the cylindrical part is 6 feet long, and the cross-sectional diameter of the tank is 2.5 feet.

9. Calculate the volume of the tank in cubic feet.

10. Verify that the tank can hold 250 gallons of liquid propane.

 

  1. https://en.wikipedia.org/wiki/Great_Pyramid_of_Giza ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Technical Mathematics Copyright © 2020 by Morgan Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.