Module 17: Angles
You will need a calculator near the end of this module.

Angle measurement is important in construction, surveying, physical therapy, and many other fields. We can visualize an angle as the figure formed when two line segments share a common endpoint. We can also think about an angle as a measure of rotation. A full rotation or a full circle is ![]() , so a half rotation or U-turn is
, so a half rotation or U-turn is ![]() , and a quarter turn is
, and a quarter turn is ![]() .
.
We often classify angles by their size.
Acute Angle: between ![]() and
and ![]()
Right Angle: exactly ![]()
Obtuse Angle: between ![]() and
and ![]()
Straight Angle: exactly ![]()
Reflexive Angle: between ![]() and
and ![]()
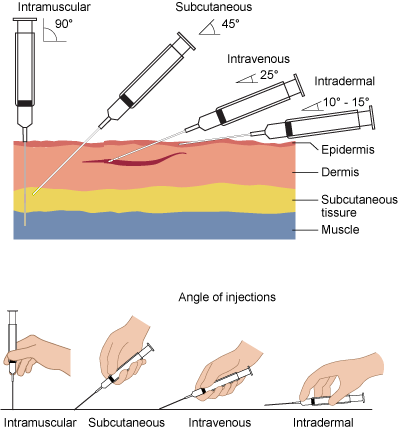
Lines that form a ![]() angle are called perpendicular. As shown below, the needle should be perpendicular to the body surface for an intramuscular injection.
angle are called perpendicular. As shown below, the needle should be perpendicular to the body surface for an intramuscular injection.
Exercises
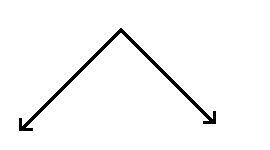
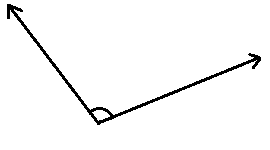
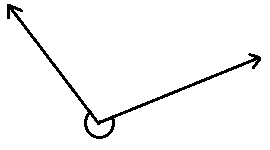
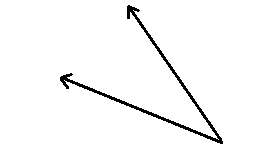
Identify each angle shown below as acute, right, obtuse, straight, or reflexive.
1. 
2. 
3. 
4. 
5. 
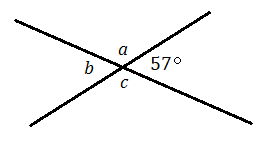
Find the measure of each unknown angle.
6. 
Angles in Triangles
If you need to find the measures of the angles in a triangle, there are a few rules that can help.
The sum of the angles of every triangle is ![]() .
.
If any sides of a triangle have equal lengths, then the angles opposite those sides will have equal measures.
Exercises
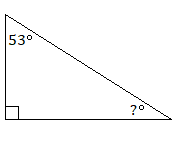
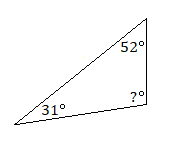
Find the measures of the unknown angles in each triangle.
7. 
8. 
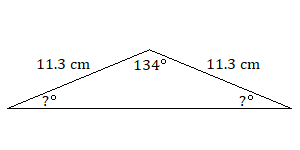
9. 
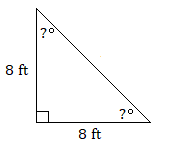
10. 
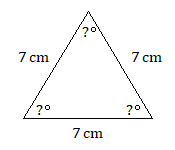
11. 
Angles and Parallel Lines
Two lines that point in the exact same direction and will never cross are called parallel lines. If two parallel lines are crossed by a third line, sets of equally-sized angles will be formed, as shown in the following diagram. All four acute angles will be equal in measure, all four obtuse angles will be equal in measure, and any acute angle and obtuse angle will have a combined measure of ![]() .
.
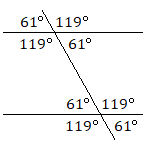
Exercises
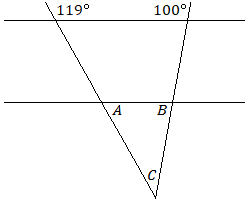
12. Find the measures of angles ![]() ,
, ![]() , and
, and ![]() .
.
Degrees, Minutes, Seconds
 It is possible to have angle measures that are not a whole number of degrees. It is common to use decimals in these situations, but the older method—called the degrees-minutes-seconds or DMS system—divides a degree using fractions out of
It is possible to have angle measures that are not a whole number of degrees. It is common to use decimals in these situations, but the older method—called the degrees-minutes-seconds or DMS system—divides a degree using fractions out of ![]() : a minute is
: a minute is ![]() of a degree, and a second is
of a degree, and a second is ![]() of a minute, which means a second is
of a minute, which means a second is ![]() of a degree. (Fortunately, these conversions work exactly like time; think of
of a degree. (Fortunately, these conversions work exactly like time; think of ![]() degree as
degree as ![]() hour.) For example,
hour.) For example, ![]() .
.
We will look at the procedure for converting between systems, but there are online calculators such as the one at https://www.fcc.gov/media/radio/dms-decimal which will do the conversions for you.
If you have latitude and longitude in DMS, like N ![]() W
W ![]() , and need to convert it to decimal degrees, the process is fairly simple with a calculator.
, and need to convert it to decimal degrees, the process is fairly simple with a calculator.
Converting from DMS to Decimal Degrees
Enter ![]() in your calculator. Round the result to the fourth decimal place, if necessary.[1]
in your calculator. Round the result to the fourth decimal place, if necessary.[1]
Exercises
Convert each angle measurement from degrees-minutes-seconds into decimal form. Round to the nearest ten-thousandth, if necessary.
13. ![]()
14. ![]()
15. ![]()
Going from decimal degrees to DMS is a more complicated process.
Converting from Decimal Degrees to DMS
- The whole-number part of the angle measurement gives the number of degrees.
- Multiply the decimal part by
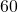 . The whole number part of this result is the number of minutes.
. The whole number part of this result is the number of minutes. - Multiply the decimal part of the minutes by
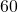 . This gives the number of seconds (including any decimal part of seconds).
. This gives the number of seconds (including any decimal part of seconds).
For example, let’s convert ![]() .
.
- The degrees part of our answer will be
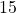 .
. - The decimal part times
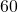 is
is 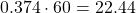 minutes. The minutes part of our answer will be
minutes. The minutes part of our answer will be 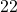 .
. - The decimal part times
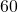 is
is 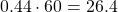 seconds. The seconds part of our answer will be
seconds. The seconds part of our answer will be 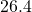 .
.
So ![]() .
.
Exercises
Convert each angle measurement from decimal into degrees-minutes-seconds form.
16. ![]()
17. ![]()
18. ![]()
- We round to four decimal places because
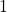 second of angle is
second of angle is 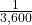 of a degree. This is a smaller fraction than
of a degree. This is a smaller fraction than 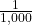 so our precision is slightly better than the thousandths place. ↵
so our precision is slightly better than the thousandths place. ↵

