Exercise Answers: Module 31

Right Triangle Trigonometry

  1. the adjacent side is e, the opposite side is f, and the hypotenuse is d.
  2. the adjacent side is x, the opposite side is y, and the hypotenuse is r.
  3. \frac{3}{5}=0.6
  4. \frac{4}{5}=0.8
  5. \frac{3}{4}=0.75
  6. \frac{4}{5}=0.8
  7. \frac{3}{5}=0.6
  8. \frac{4}{3}\approx1.333
  9. 0.6000
  10. 0.8000
  11. 0.7500
  12. 0.8000
  13. 0.6000
  14. 1.333
  15. z\approx4.6\text{ cm}
  16. g\approx2.6\text{ cm}
  17. b\approx5.706\text{ in}
  18. p\approx75.51\text{ mm}
  19. y\approx136.18\text{ mm}
  20. d\approx296.87\text{ mm}
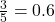
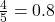
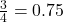
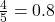
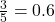
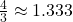
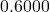
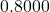
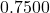
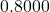
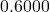
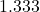
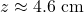
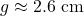
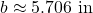
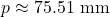
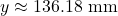
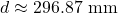
  21. the wire is approximately 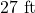27\text{ ft} long
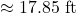  22. \approx17.85\text{ ft}, which is roughly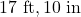 17\text{ ft}, 10\text{ in}
  23. No; 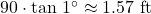90\cdot\text{tan }1^\circ\approx1.57\text{ ft}, so the puck will hit the plywood over 1.5 feet away from the center of the hole.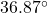
  24. 36.87^\circ
  25. 60^\circ
  26. 53.13^\circ
  27. \angle A\approx36.47^\circ
  28. \angle1\approx42.03^\circ
  29. \angle1\approx30.76^\circ
  30. \angle y\approx52.88^\circ
  31. \angle1\approx55.28^\circ
  32. \angle x\approx31.50^\circ; \angle y\approx58.50^\circ
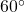
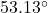
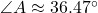
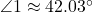
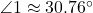
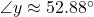
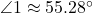
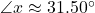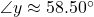
  33. Yes; 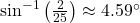\text{sin}^{-1}\left(\frac{2}{25}\right)\approx4.59^\circ, which is less than 4.75^\circ.
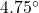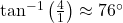  34. \text{tan}^{-1}\left(\frac{4}{1}\right)\approx76^\circ angle of elevation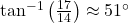
  35. \text{tan}^{-1}\left(\frac{17}{14}\right)\approx51^\circ
  36. 17\div\text{sin }51^\circ\approx21.9
  37. 14\div\text{cos }51^\circ\approx22.2
  38. \sqrt{14^2+17^2}\approx22.0
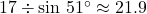
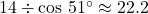
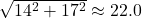
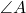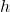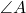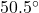  39. You were told to round off the measure of \angle A to the nearest degree, which introduced some round-off error when you subsequently used sine or cosine to determine h based on that angle. We would need to round \angle A to 50.5^\circ instead of 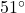51^\circ if we want the three results to agree to the nearest tenth. 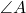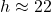By rounding \angle A to the nearest degree, we decreased the precision of the first two answers to the nearest whole number (h\approx22).

 

return to main page

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Technical Mathematics Copyright © 2020 by Morgan Chase is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.