Module 6: Precision and GPE
Precision
The precision of a number is the place value of the rightmost significant figure. For example, ![]() is precise to the hundredths place, and
is precise to the hundredths place, and ![]() is precise to the tens place.
is precise to the tens place.
Exercises
Identify the precision (i.e., the place value of the rightmost significant figure) of each number.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
Precision-Based Rounding
In a previous module about decimals, we used precision-based rounding because we were rounding to a specified place value; for example, rounding to the nearest tenth. Let’s practice this with overbars and trailing zeros.
Precision-based rounding:
-
Locate the rounding digit in the place to which you are rounding.
-
Look at the test digit directly to the right of the rounding digit.
-
If the test digit is 5 or greater, increase the rounding digit by 1 and drop all digits to its right. If the test digit is less than 5, keep the rounding digit the same and drop all digits to its right.
Remember, when the rounding digit of a whole number is a ![]() that gets rounded up to a
that gets rounded up to a ![]() , we must write an overbar above that
, we must write an overbar above that ![]() .
.
Also, when the rounding digit of a decimal number is a ![]() that gets rounded up to a
that gets rounded up to a ![]() , we must include the
, we must include the ![]() in that decimal place.
in that decimal place.
Exercises
Round each number to the indicated place value. Be sure to include trailing zeros or an overbar if necessary.
11. ![]() (thousands)
(thousands)
12. ![]() (hundreds)
(hundreds)
13. ![]() (tens)
(tens)
14. ![]() (tenths)
(tenths)
15. ![]() (hundredths)
(hundredths)
16. ![]() (thousandths)
(thousandths)
Precision when Adding and Subtracting
Suppose the attendance at a large event is estimated at ![]() people, but then you see
people, but then you see ![]() people leave. Is the new estimate
people leave. Is the new estimate ![]() ? No, because the original estimate was precise only to the nearest thousand. We can’t start with an imprecise number and finish with a more precise number. If we estimated that
? No, because the original estimate was precise only to the nearest thousand. We can’t start with an imprecise number and finish with a more precise number. If we estimated that ![]() people had left, then we could revise our attendance estimate to
people had left, then we could revise our attendance estimate to ![]() because this estimate maintains the same level of precision as our original estimate.
because this estimate maintains the same level of precision as our original estimate.
Don’t round off the original numbers; do the necessary calculations first, then round the answer as your last step.
Exercises
Add or subtract as indicated. Round to the appropriate level of precision.
17. Find the combined weight of four packages with the following weights: ![]() lb,
lb, ![]() lb,
lb, ![]() lb,
lb, ![]() lb.
lb.
18. Find the combined weight of four packages with the following weights: ![]() lb,
lb, ![]() lb,
lb, ![]() lb,
lb, ![]() lb.
lb.
19. While purchasing renter’s insurance, Chandra estimates the value of her insurable possessions at $ ![]() . After selling some items valued at $
. After selling some items valued at $ ![]() , what would be the revised estimate?
, what would be the revised estimate?
20. Chandra knows that she has roughly $ ![]() in her checking account. After using her debit card to make two purchases of $
in her checking account. After using her debit card to make two purchases of $ ![]() and $
and $ ![]() , how much would she have left in her account?
, how much would she have left in her account?
 If you are multiplying by an exact number, you can consider this a repeated addition. For example, suppose you measure the weight of an object to be
If you are multiplying by an exact number, you can consider this a repeated addition. For example, suppose you measure the weight of an object to be ![]() ounces and you want to know the weight of three of these objects; multiplying
ounces and you want to know the weight of three of these objects; multiplying ![]() times
times ![]() is the same as adding
is the same as adding ![]() ounces. The precision is still to the hundredths place. The issue of significant figures doesn’t apply to exact numbers, so it would be wrong to treat
ounces. The precision is still to the hundredths place. The issue of significant figures doesn’t apply to exact numbers, so it would be wrong to treat ![]() as having only one sig fig. (Treat exact numbers like royalty; their precision is perfect and it would be an insult to even question it.)
as having only one sig fig. (Treat exact numbers like royalty; their precision is perfect and it would be an insult to even question it.)
Greatest Possible Measurement Error (GPE)
Suppose you are weighing a dog with a scale that displays the weight rounded to the nearest pound. If the scale says Sir Barks-A-Lot weighs ![]() pounds, he could weigh anywhere from
pounds, he could weigh anywhere from ![]() pounds to almost
pounds to almost ![]() pounds. The true weight could be as much as
pounds. The true weight could be as much as ![]() pounds above or below the measured weight, which we could write as
pounds above or below the measured weight, which we could write as ![]() .
.
Now suppose you are weighing Sir Barks-A-Lot with a scale that displays the weight rounded to the nearest tenth of a pound. If the scale says Sir Barks-A-Lot weighs ![]() pounds, we now know that he could weigh anywhere from
pounds, we now know that he could weigh anywhere from ![]() pounds to almost
pounds to almost ![]() pounds. The true weight could be as much as
pounds. The true weight could be as much as ![]() pounds above or below the measured weight, which we could write as
pounds above or below the measured weight, which we could write as ![]() .
.
As we increase the level of precision in our measurement, we decrease the greatest possible measurement error or GPE. The GPE is always one half the precision; if the precision is to the nearest tenth, ![]() , the GPE is half of one tenth, or five hundredths,
, the GPE is half of one tenth, or five hundredths, ![]() . The GPE will always be a
. The GPE will always be a ![]() in the place to the right of the place value of the number’s precision.
in the place to the right of the place value of the number’s precision.
Another way to think about the GPE is that it gives the range of values that would round off to the number in question. Back to weighing Sir Barks-A-Lot: ![]() tells us a lower value and an upper value.
tells us a lower value and an upper value. ![]() is the lowest weight that would round up to
is the lowest weight that would round up to ![]() . Similarly,
. Similarly, ![]() is the highest weight that would round down to
is the highest weight that would round down to ![]() . Yes, perhaps we should say
. Yes, perhaps we should say ![]() or
or ![]() , etc., for the upper limit here, but it is easier to just say
, etc., for the upper limit here, but it is easier to just say ![]() and agree that
and agree that ![]() is the upper limit even though it would round up instead of down. Using inequalities, we could represent
is the upper limit even though it would round up instead of down. Using inequalities, we could represent ![]() as the range of values
as the range of values ![]() instead.
instead.
 When you are asked to identify the GPE, it may help to think “What are the minimum and maximum numbers that would round to the given number?” For example, suppose the attendance at a Portland Thorns match is estimated to be
When you are asked to identify the GPE, it may help to think “What are the minimum and maximum numbers that would round to the given number?” For example, suppose the attendance at a Portland Thorns match is estimated to be ![]() people. This number is precise to the nearest thousand. The minimum number that would round up to
people. This number is precise to the nearest thousand. The minimum number that would round up to ![]() would be
would be ![]() (because
(because ![]() would round down to
would round down to ![]() ), and the maximum number that would round down to
), and the maximum number that would round down to ![]() would be just below
would be just below ![]() (because
(because ![]() would round up to
would round up to ![]() ). Because these numbers are each
). Because these numbers are each ![]() away from
away from ![]() , the GPE is
, the GPE is ![]() . If the estimate of
. If the estimate of ![]() is correct to the nearest thousand, we know that the actual attendance is within
is correct to the nearest thousand, we know that the actual attendance is within ![]() 500 of
500 of ![]() .
.
Exercises
21. A package weighs ![]() pounds. What is the GPE?
pounds. What is the GPE?
22. A roll of plastic sheeting is ![]() inches thick. What is the GPE in inches?
inches thick. What is the GPE in inches?
23. Plastic sheeting ![]() inches thick is referred to as
inches thick is referred to as ![]() mil. What is the GPE in mils?
mil. What is the GPE in mils?
Recall from the previous module that the accuracy of a measurement is the number of significant figures. Let’s put together the ideas of accuracy, precision, and greatest possible measurement error.
Exercises
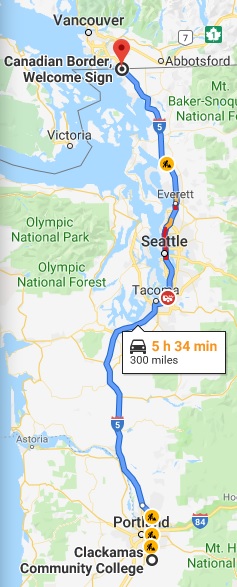
Google Maps says that the driving distance from CCC’s main campus to the Canadian border is ![]() miles. (Note: this is rounded to the nearest mile.)
miles. (Note: this is rounded to the nearest mile.)
24. What is the accuracy?
25. What is the precision?
26. What is the GPE?
A new stadium is expected to have around ![]() seats.
seats.
27. What is the accuracy?
28. What is the precision?
29. What is the GPE?
The capacity of a car’s gas tank is ![]() gallons.
gallons.
30. What is the accuracy?
31. What is the precision?
32. What is the GPE?
Here is a summary of the important terms from these two modules. It is easy to get them mixed up, but remembering that “precision” and “place value” both start with “p” can be helpful.
Summary of Terms
Significant figures: the digits in a number that we trust to be correct
Accuracy: the number of significant digits
Precision: the place value of the rightmost significant digit
Greatest possible measurement error (GPE): one half the precision

