Module 34: Radian Measure
You may use a calculator as needed in this module.
 In everyday life, we measure angles in degrees. However, degrees are an arbitrary unit of measure; why is a right angle 90 degrees and a full circle 360 degrees?[1]
In everyday life, we measure angles in degrees. However, degrees are an arbitrary unit of measure; why is a right angle 90 degrees and a full circle 360 degrees?[1]
Another unit that is used in surveying is the gradian; a right angle is equal to 100 gradians. Using gradians makes some calculations easier, but this is still an arbitrary unit of measure.
In this module, we will focus on a third unit of angle measure known as radians.
Radian Measure
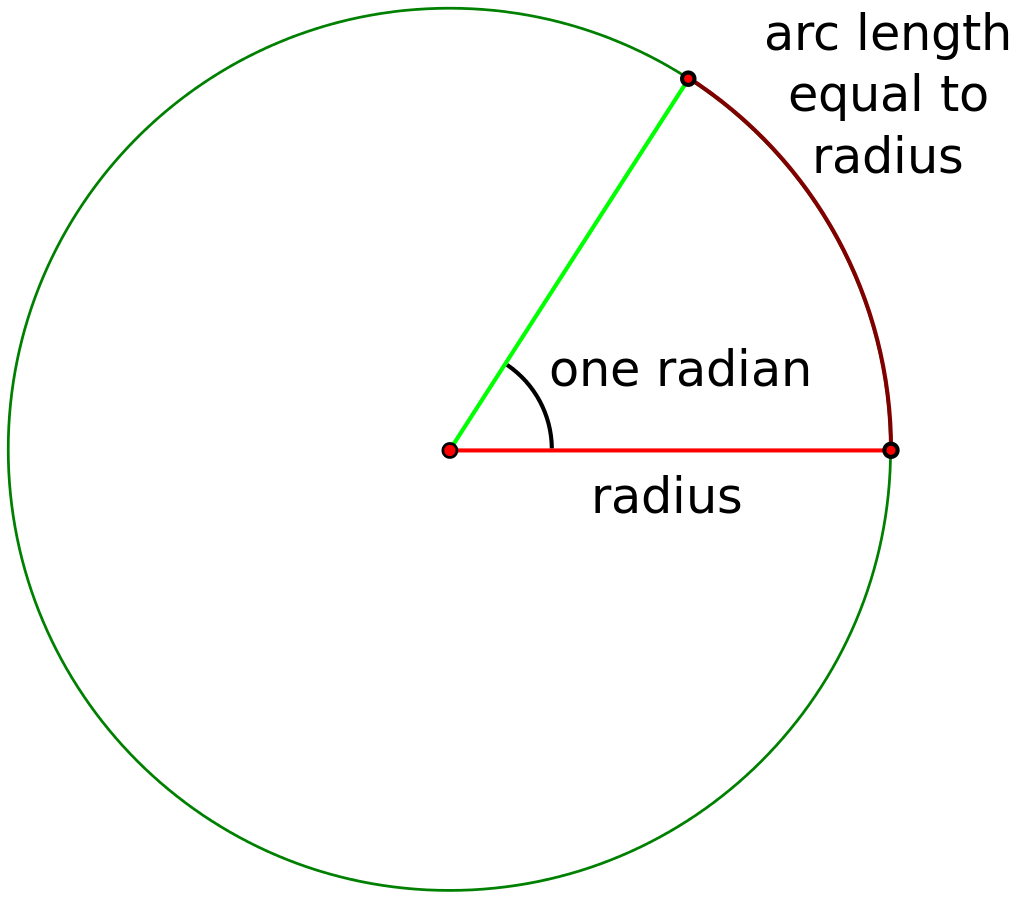
To explain radian measure, we can visualize a circle. Next, let’s measure a length along the circumference of a circle that is equal to the radius. Finally, let’s draw an angle with its vertex at the center of the circle, intersecting the circle at the endpoints of this arc. The measure of this angle is defined to be 1 radian.
In fewer words, a radian is the measure of the central angle that forms an arc equal to the circle’s radius.
Because the circumference of a circle is ![]() times the radius, there are
times the radius, there are ![]() radians in one full circle, and therefore
radians in one full circle, and therefore ![]() radians are equivalent to
radians are equivalent to ![]() .
.

![]()
![]()
We can convert between degrees and radians using the conversion factor ![]() .
.
Exercises
Convert each degree measure into radian measure. Leave your answers in terms of ![]() .
.
Convert each radian measure into degree measure.
- See https://en.wikipedia.org/wiki/Degree_(angle)#History for some theories. ↵

