Module 5: Accuracy and Significant Figures
 In the first few modules, we rarely concerned ourselves with rounding; we assumed that every number we were told was exact and we didn’t have to worry about any measurement error. However, every measurement contains some error. A standard sheet of paper is
In the first few modules, we rarely concerned ourselves with rounding; we assumed that every number we were told was exact and we didn’t have to worry about any measurement error. However, every measurement contains some error. A standard sheet of paper is ![]() inches wide and
inches wide and ![]() inches high, but it’s possible that the actual measurements could be closer to
inches high, but it’s possible that the actual measurements could be closer to ![]() and
and ![]() inches. Even if we measure something very carefully, with very sensitive instruments, we should assume that there could be some small measurement error.
inches. Even if we measure something very carefully, with very sensitive instruments, we should assume that there could be some small measurement error.
Exact Values and Approximations
A number is an exact value if it is the result of counting or a definition.
A number is an approximation if it is the result of a measurement or of rounding.
Exercises
Identify each number as an exact value or an approximation.
1. An inch is ![]() of a foot.
of a foot.
2. This board is ![]() inches long.
inches long.
3. There are ![]() students in class.
students in class.
4. A car’s tachometer reads ![]() rpm.
rpm.
5. A right angle measures ![]() °.
°.
6. The angle of elevation of a ramp is ![]() °.
°.
Suppose a co-worker texts you that they will arrive in ![]() minutes. It’s hard to tell how precise this number is, because we often round off to the nearest
minutes. It’s hard to tell how precise this number is, because we often round off to the nearest ![]() or
or ![]() minutes. You might reasonably expect them to arrive anytime within the next
minutes. You might reasonably expect them to arrive anytime within the next ![]() to
to ![]() minutes. If your co-worker texts that they will arrive in
minutes. If your co-worker texts that they will arrive in ![]() minutes, though, it is likely that their GPS told them that more precise number, and you could reasonably expect them to arrive within
minutes, though, it is likely that their GPS told them that more precise number, and you could reasonably expect them to arrive within ![]() to
to ![]() minutes.
minutes.
Accuracy and Significant Figures

Because measurements are inexact, we need to consider how accurate they are. This requires us to think about significant figures—often abbreviated “sig figs” in conversation—which are the digits in the measurement that we trust to be correct. The accuracy of a number is equal to the number of significant figures.[1] The following rules aren’t particularly difficult to understand but they can take time to absorb and internalize, so we’ll include lots of examples and exercises.
Significant Figures
- All nonzero digits are significant.
Ex: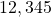 has five sig figs, and
has five sig figs, and 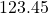 has five sig figs.
has five sig figs. - All zeros between other nonzero digits are significant.
Ex: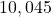 has five sig figs, and
has five sig figs, and 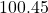 has five sig figs.
has five sig figs. - Any zeros to the right of a decimal number are significant.
Ex: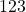 has three sig figs, but
has three sig figs, but 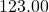 has five sig figs.
has five sig figs. - Zeros on the left of a decimal number are NOT significant.
Ex: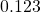 has three sig figs, and
has three sig figs, and 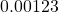 has three sig figs.
has three sig figs. - Zeros on the right of a whole number are NOT significant unless they are marked with an overbar.
Ex: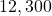 has three sig figs, but
has three sig figs, but 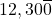 has five sig figs.
has five sig figs.
Another way to think about #4 and #5 above is that zeros that are merely showing the place value—where the decimal point belongs—are NOT significant.
Exercises
Determine the accuracy (i.e., the number of significant figures) of each number.
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
Exercises
Determine the accuracy (i.e., the number of significant figures) of each number.
13. ![]()
14. ![]()
15. ![]()
16. ![]()
Two things to remember: we don’t put an overbar over a nonzero digit, and we don’t need an overbar for any zeros on the right of a decimal number because those are already understood to be significant.
Accuracy-Based Rounding
As we saw in a previous module about decimals, it is often necessary to round a number. We often round to a certain place value, such as the nearest hundredth, but there is another way to round. Accuracy-based rounding considers the number of significant figures rather than the place value.
Accuracy-based rounding:
-
Locate the rounding digit to which you are rounding by counting from the left until you have the correct number of significant figures.
-
Look at the test digit directly to the right of the rounding digit.
-
If the test digit is 5 or greater, increase the rounding digit by 1 and drop all digits to its right. If the test digit is less than 5, keep the rounding digit the same and drop all digits to its right.
Exercises
Round each number so that it has the indicated number of significant figures.
17. ![]() (two sig figs)
(two sig figs)
18. ![]() (three sig figs)
(three sig figs)
19. ![]() (four sig figs)
(four sig figs)
20. ![]() (two sig figs)
(two sig figs)
21. ![]() (three sig figs)
(three sig figs)
22. ![]() (four sig figs)
(four sig figs)
When the rounding digit of a whole number is a ![]() that gets rounded up to a
that gets rounded up to a ![]() , we must write an overbar above that
, we must write an overbar above that ![]() .
.
Similarly, when the rounding digit of a decimal number is a ![]() that gets rounded up to a
that gets rounded up to a ![]() , we must include the
, we must include the ![]() in that decimal place.
in that decimal place.
Exercises
Round each number so that it has the indicated number of significant figures. Be sure to include trailing zeros or an overbar if necessary.
23. ![]() (two sig figs)
(two sig figs)
24. ![]() (three sig figs)
(three sig figs)
25. ![]() (four sig figs)
(four sig figs)
26. ![]() (two sig figs)
(two sig figs)
27. ![]() (three sig figs)
(three sig figs)
28. ![]() (four sig figs)
(four sig figs)

The mountain we know as Mt. Everest is called Sagarmatha in Nepal and Chomolungma in Tibet. On December 8, 2020, it was jointly announced by Nepal and China that the summit has an elevation of ![]() ft, replacing the previously accepted elevation of
ft, replacing the previously accepted elevation of ![]() ft.[3]
ft.[3]
29. Round ![]() ft to two sig figs.
ft to two sig figs.
30. Round ![]() ft to three sig figs.
ft to three sig figs.
31. Round ![]() ft to four sig figs.
ft to four sig figs.
32. Round ![]() ft to five sig figs.
ft to five sig figs.
33. Round ![]() ft to six sig figs.
ft to six sig figs.
Accuracy when Multiplying and Dividing
Suppose you needed to square the number ![]() . You could rewrite
. You could rewrite ![]() as the improper fraction
as the improper fraction ![]() and then figure out that
and then figure out that ![]() , which equals the repeating decimal
, which equals the repeating decimal ![]()
Because most people prefer decimals to fractions, we might instead round ![]() to
to ![]() and find that
and find that ![]() . However, this is not accurate because
. However, this is not accurate because ![]() rounded to the nearest hundredth should be
rounded to the nearest hundredth should be ![]() . The answer
. The answer ![]() looks very accurate, but it is a false accuracy because there is round-off error involved. If we round our answer
looks very accurate, but it is a false accuracy because there is round-off error involved. If we round our answer ![]() to the nearest tenth, we would get
to the nearest tenth, we would get ![]() , which is still not accurate because
, which is still not accurate because ![]() rounded to the nearest tenth should be
rounded to the nearest tenth should be ![]() . If we round our answer
. If we round our answer ![]() to the nearest whole number, we would get
to the nearest whole number, we would get ![]() , which is accurate because
, which is accurate because ![]() rounded to the nearest whole number is indeed
rounded to the nearest whole number is indeed ![]() . It turns out that we should be focusing on the number of significant figures rather than the place value; because
. It turns out that we should be focusing on the number of significant figures rather than the place value; because ![]() has only two sig figs, our answer must be rounded to two sig figs.
has only two sig figs, our answer must be rounded to two sig figs.
Suppose instead that we round ![]() to
to ![]() and find that
and find that ![]() . Again, this is not accurate because
. Again, this is not accurate because ![]() rounded to the nearest ten-thousandth should be
rounded to the nearest ten-thousandth should be ![]() . If we round
. If we round ![]() to the nearest thousandth, we would get
to the nearest thousandth, we would get ![]() , which is still not accurate because
, which is still not accurate because ![]() rounded to the nearest thousandth should be
rounded to the nearest thousandth should be ![]() . If we round
. If we round ![]() to the nearest hundredth, we would get
to the nearest hundredth, we would get ![]() , which is still not accurate because
, which is still not accurate because ![]() rounded to the nearest hundredth should be
rounded to the nearest hundredth should be ![]() . Only when we round to the nearest tenth do we get an accurate result:
. Only when we round to the nearest tenth do we get an accurate result: ![]() rounded to the nearest tenth is
rounded to the nearest tenth is ![]() , which is accurate because
, which is accurate because ![]() rounded to the nearest tenth is indeed
rounded to the nearest tenth is indeed ![]() . As above, we need to focus on the number of significant figures rather than the place value; because
. As above, we need to focus on the number of significant figures rather than the place value; because ![]() has only three sig figs, our answer must be rounded to three sig figs.
has only three sig figs, our answer must be rounded to three sig figs.
Don’t round off the original numbers; do the necessary calculations first, then round the answer as your last step.
Exercises
Use a calculator to multiply or divide as indicated. Then round to the appropriate level of accuracy.
34. ![]()
35. ![]()
36. ![]()
37. ![]()
38. Suppose you are filling a 5-gallon can of gasoline. The gasoline costs $2.579 per gallon, and you estimate that you will buy ![]() gallons. How much should you expect to spend?
gallons. How much should you expect to spend?
- The terms "significant digits" and "significant figures" are used interchangeably. ↵
- Precision is different from accuracy, as we'll learn in the next module, but it is mentioned here because it can be difficult to explain one without the other. ↵
- https://www.washingtonpost.com/world/asia_pacific/mount-everest-height-nepal-china/2020/12/08/a7b3ad1e-389a-11eb-aad9-8959227280c4_story.html ↵

