32 Under Water Weight
Apparent Weight
When an object is held still under water it appears to weigh less than it does in air because the buoyant force is helping to hold it up (balance its weight). For this reason, the reduced force you need to apply to hold the object is known as the apparent weight. When a scale is used to weigh an object submerged in water the scale will read the apparent weight. When performing hydrostatic weighing for body composition measurement the apparent weight is often called the under water weight (![]() ).
).
Static Equilibrium
When weighing under water we know the buoyant force must be equal to the difference between the weight and apparent weight because the object remains still, which is a state known as static equilibrium. For an object to be in static equilibrium, all of the forces on it must be balanced so that there is no net force. For the case of under water weighing, the buoyant force plus the force provided by the scale must perfectly balance the weight of the object, as long as the object is holding still. We can use arrows to represent the forces on an object and visualize how they are balanced or unbalanced. This type of diagram is known as a free body diagram (FBD). The direction of arrows shows the direction of the forces and the arrow lengths shows the size (magnitude) of the force. In this case we call the arrows vectors and say the forces they represent are vector quantities. The FBD for a person undergoing hydrostatic weighing would look like this:
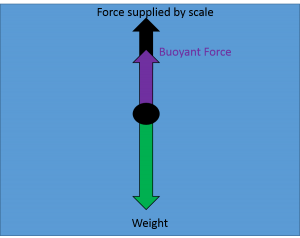
We learned in the last chapter that scales measure the force that they are supplying to other objects. The scale must supply less restoring force to counteract weight and maintain static equilibrium when the buoyant force is also helping, therefore the scale will provide a apparent weight reading that is less than the actual weight.
Archimedes’ Principle
Measuring the weight and apparent weight of a body allows us to calculate its density because the buoyant force that causes the reduction in apparent weight has a special relation to the amount of water being displaced by the body. Archimedes' Principle states that the buoyant force provided by a fluid is equal to the weight of the fluid displaced.
Reinforcement Exercises
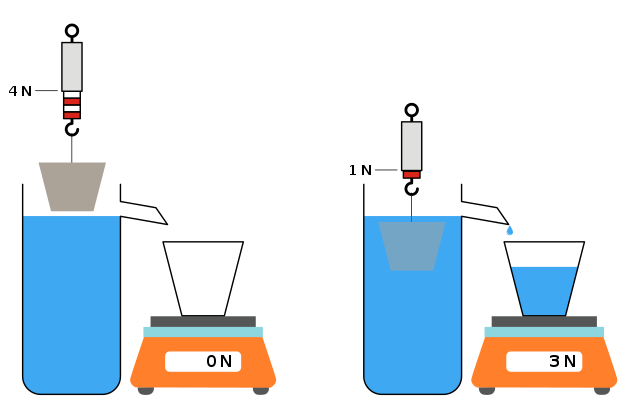
Buoyant Force and Density
A given mass of low density tissue will take up volume relative to the same mass of high density tissue. Taking up the volume means more water is displaced when the body is submerged so the buoyant force will be larger compared to the weight than it would be for a more dense body. In turn, that means that apparent weight is smaller relative to actual weight for bodies of higher density. By comparing weight and apparent weight, the body density can be determined. We will do that in the next chapter, but first we should become more familiar with the Buoyant force.
Everyday Example
The water displaced by a brick weighs less than the brick so the buoyant force cannot cancel out the weight of the brick and it will tend to sink (left diagram). To hold the brick in place you must provide the remaining upward force to balance the weight and maintain static equilibrium. That force is less than the weight in air so the brick appears to weigh less in the water (right diagram).
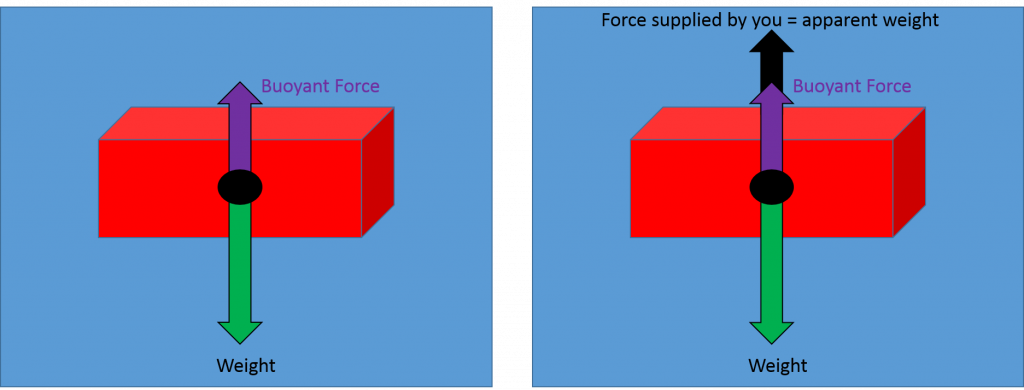
If you let go of the brick it will be out of equilibrium and sink to the pool bottom. At that point the pool bottom is providing the extra upward force to balance out the weight, and the brick is once again in static equilibrium.
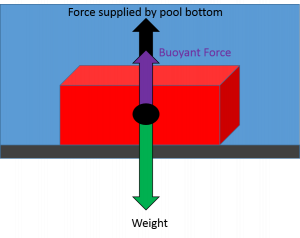
The water displaced by an entire beach ball weighs more than a beach ball, so if you hold one under water the buoyant force will be greater than the weight. Your hand is providing the extra downward force to balance out the forces and maintain static equilibrium (left diagram). When you let go, the forces will be unbalanced and the ball will begin moving upward (right diagram).

The density of ice is only about 9/10 that of water. The weight of the water displaced by only 9/10 of the iceberg has the same weight as the entire iceberg. Therefore, 1/10 of the iceberg must remain exposed in order for the weight and buoyant forces to be balanced and the iceberg to be in static equilibrium.

Reinforcement Exercises
Check out this buoyancy simulation which lets you control how much objects of different masses are submerged and shows you the resulting buoyant force along with forces provided by you and a scale at the bottom of the pool (apparent weight).
Not-So-Everyday Example
Submarines control how much water they displace by pumping water in and out of tanks within the submarine. When water is pumped inside, then that water is not displaced by the sub and it doesn’t count toward increasing the buoyant force. Conversely, when water is pumped out that water is now displaced by the sub and the buoyant force increases, which is the concept behind the maneuver in the following video:
- "Archimedes-principle"By MikeRun [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)], from Wikimedia Commons ↵
- "Iceberg" created by Uwe Kils (iceberg) and User:Wiska Bodo (sky). [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/)], via Wikimedia Commons ↵
the upward force exerted by any fluid upon a body placed in it
the force of gravity on on object, typically in reference to the force of gravity caused by Earth or another celestial body
the reading on a scale that is used to measure the weight of an object that is submerged in a fluid
a technique for measuring the mass per unit volume of a living person's body. It is a direct application of Archimedes' principle, that an object displaces its own volume of water
apparent weight when submerged in water
the state being in equilibrium (no unbalanced forces or torques) and also having no motion
the total amount of remaining unbalanced force on an object
a graphical illustration used to visualize the forces applied to an object
the size or extent of a vector quantity, regardless of direction
a quantity having direction as well as magnitude
a force that tends to move a system back toward the equilibrium position
relation between the amount of a material and the space it takes up, calculated as mass divided by volume.
pushed out of original position, typically in reference to fluid pushed out of the way by an object placed in the fluid, or an object being displaced from its equilibrium position
The upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially submerged, is equal to the weight of the fluid being displaced by the body
a measurement of the amount of matter in an object made by determining its resistance to changes in motion (inertial mass) or the force of gravity applied to it by another known mass from a known distance (gravitational mass). The gravitational mass and an inertial mass appear equal.
a quantity of space, such as the volume within a box or the volume taken up by an object.
a state of having no unbalanced forces or torques