In the previous chapter we found the biceps tension force in our example problem to be 430 lbs! You may have noticed that when we found the biceps tension we completely ignored the forces acting at the elbow joint. We were allowed to do this because those forces cause no torque.  Forces  acting on the fulcrum of a lever don’t cause the lever to rotate.  Just because the forces on the elbow don’t cause rotation, that doesn’t mean they aren’t important. Those forces can certainly damage the joint if they get too large. Let’s try to find out how big those forces are for our example problem.

^[1]

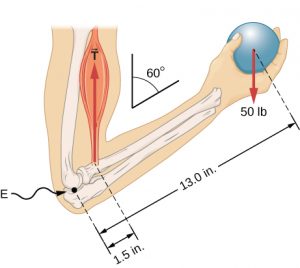
The forearm is holding still and not moving so it must be in static equilibrium and all the vertical forces must be canceling out. If the vertical forces didn’t cancel out the forearm would begin to move up or down.  We already know that the weight of the ball is 50 lbs downward and the bicep tension is 433 lbs upward. The downward weight cancels 50 lbs worth of the upward muscle tension, leaving behind a remaining 383 lbs of upward force. The forearm is in static equilibrium, so the vertical force on the end of the forearm at the elbow must cancel out this 383 lbs upward force,  meaning that the vertical force on the elbow end of the forearm is 383 lbs downward. This force comes from the upper arm bone (humerus) pushing down on the end of the forearm bones (radius and ulna). Adjusting our significant figures, we should report this force as 380 lbs.

Horizontal Elbow Forces

The horizontal forces must all cancel out because the forearm is in static equilibrium, but there are no horizontal forces in our example to begin with, so that’s it. We’re finished analyzing the forces on the forearm while holding a 50 lb ball!