Tipping

Materials:

• writing utensil
• calculator
• digital device with spreadsheet program
• digital device with internet access

Observation

According to unit 5, weight, static friction, and normal force must be balanced in all directions in order for a body to remain in static equilibrium. The following video shows how to predict the maximum slope for which an object will not tip. The result depends only on the center of mass height () and horizontal distance ()from the center of mass to the edge of the support base:

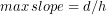• • , or in terms of the slope angle,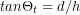 

Questions

The above model assume that only gravity, friction, and normal force act on the object and that the center of gravity is the same as the center of mass. Are these assumptions reasonable? Can the models correctly predict the slope beyond which tipping occurs for an object such as the human body?

Search Existing Knowledge

1) Can you find any existing information that helps to answer our question? Explain below, and cite your sources.

Hypothesis Generation:

2) We need to turn our question into a set of  testable statements such that the results of testing the statements will provide evidence that helps us to answer the question. Choosing a % difference that is very large might ensure that your hypothesis is supported by the data, but that result would not provide evidence that the model is valid. Such a hypothesis would not be very useful. Instead, choose a % difference that would give strong evidence the values are the same if you hypothesis is confirmed.

• If the assumptions are reasonable and the tipping model is valid, then the experimentally determined maximum slope before ___________ occurs will be less than _________% different from .

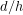3) Explain your choice of % difference for your hypotheses.

Experimental Hypothesis Testing

General Overview of Experimental Procedure

1. Find the center of mass height (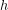) and distance from center of mass to support base edge ().
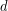2. Calculate the predicted max slope before tipping as .
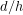3. Measure the slope angle at which each object begins to tip.
4. Find the slope by calculating the tangent of the slope angle (slope = )
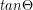5. Compare the values of the measured and predicted max slope and see if they match to within % difference you chose in your hypothesis.

4) Calculate the center of mass height according to the method described in the video below. Record your results of the calculation here:

5) Record the value of the horizontal distance from center of mass to edge of support base, as discussed in the video above.

6) According to the video on tipping, the maximum slope before tipping is equal to . Use your values above to predict the slope at which the object will tip.

15) Watch the following video and record the maximum tipping angle.

7) Calculate the tangent of the tipping angle to get the slope.

8) Compare the measured slope to the experimentally determined slope by calculating a percent difference. Cite any sources you used to find information on calculating percent difference.

Conclusions

9) Do the results support or refute your second hypothesis?

10) With regard to our original question, do our data and conclusions provide evidence that the tipping model derived in the first video is valid?