84 Efficiency of the Human Body

The Energetic Functions of the Body[1]

An f M R I scan of a human head with energy consumption in the vision center shown by a bright spot. This brightness indicates the energy consumption.
This fMRI scan shows an increased level of energy consumption in the vision center of the brain. Here, the patient was being asked to recognize faces. Image credit: NIH via Wikimedia Commons

All bodily functions, from thinking to lifting weights, require energy. The many small muscle actions accompanying all quiet activity, from sleeping to head scratching, ultimately become thermal energy, as do less visible muscle actions by the heart, lungs, and digestive tract. The rate at which the body uses food energy to sustain life and to do different activities is called the metabolic rate. The total energy conversion rate of a person at rest is called the basal metabolic rate (BMR) and is divided among various systems in the body, as shown the following table:

Basal Metabolic Rates (BMR)
Organ Power consumed at rest (W) Oxygen consumption (mL/min) Percent of BMR
Liver & spleen 23 67 27
Brain 16 47 19
Skeletal muscle 15 45 18
Kidney 9 26 10
Heart 6 17 7
Other 16 48 19
Totals 85 W 250 mL/min 100%
The largest fraction of energy goes to the liver and spleen, with the brain coming next.  About 75% of the calories burned in a day go into these basic functions. A full 25% of all basal metabolic energy consumed by the body is used to maintain electrical potentials in all living cells. (Nerve cells use this electrical potential in nerve impulses.) This bioelectrical energy ultimately becomes mostly thermal energy, but some is utilized to power chemical processes such as in the kidneys and liver, and in fat production. The BMR is a function of age, gender, total body weight, and amount of muscle mass (which burns more calories than body fat). Athletes have a greater BMR due to this last factor.  Of course, during vigorous exercise, the energy consumption of the skeletal muscles and heart increase markedly. The following diagram summarizes the basic energetic functioning in the human body.
A box labeled "the body does work" has an arrow labeled "input" pointing inward from the left. The arrow starts from a box labeled "Chemical Potential Energy." An arrow labeled "output" points outward from the body box to the right and toward a pair of boxes labeled "Potential Energy" and "Kinetic Energy." The potential energy box contains the terms "chemical, electrical, spring, gravitational." The terms chemical and electrical are connected to the terms "growth/repair, nerve function, cellular metabolism, storage." The terms spring, gravitational, and kinetic energy are connected to the the term "motion." An arrow labeled "heat" points outward and upward from the top of the central purple box and toward a box labeled "thermal energy." Small, thin arrows connect the output and input arrows to the word "efficiency," and separately the input and heat arrows to the word "entropy."
The most basic functions of the human body mapped to the main concepts covered in this textbook.(Chemical potential energy is actually a form of electric potential energy, but we will not specifically discuss electric potential energy in this textbook so we have separated the two.)

 

The First Law of Thermodynamics

Heat

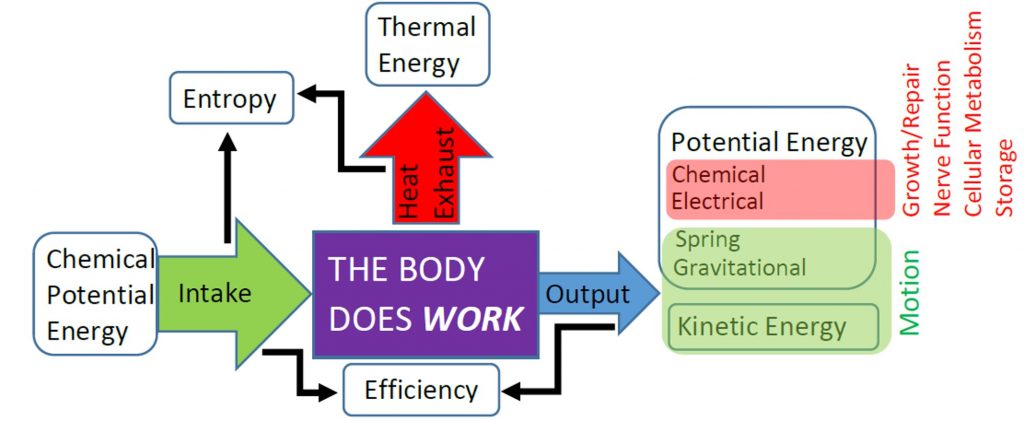
The body is capable of storing chemical potential energy and thermal energy internally. Remembering that thermal energy is just the kinetic energy of atoms and molecules, we recognize that these two types of energy are stored microscopically and internal to the body. Therefore, we often lump these two types of microscopic energy into the internal energy (U). When on object is warmer then its surroundings then thermal energy will be transferred from object to surroundings, but if the object is cooler than its surroundings then thermal energy will transferred into the object from its surroundings. The amount of thermal energy exchanged due to temperature differences is often called heat (Q). When heat is transferred out of the body to the environment, we say call this exhaust heat, as indicated in the previous figure.  We will learn more about how temperature and heat transfer are related in the next unit.

Energy Conservation

The Principle of Conservation of Energy states that energy cannot be created or destroyed. Therefore, if the body does useful work to transfer mechanical energy to its surroundings (W_{by}), or transfer thermal energy to the environment as heat, then that energy must have come out of the body’s internal energy. We observe this throughout nature as the First Law of Thermodynamics:

(1)   \begin{equation*} \Delta U = Q - W_{by} \end{equation*}

Heat Engines

Your body uses chemical potential energy stored internally to do work, and that process also generates thermal energy, which you release as exhaust heat. The internal combustion engines that power most cars operate in similar fashion by converting chemical potential energy in fuel to thermal energy via combustion, then converting some of the thermal energy into useful work and dumping some into exhaust heat. Your body is capable of releasing the chemical potential energy in your food without combustion, which is good, because you are not capable of  using thermal energy your from yourinternal energy to do work. Machines that can use thermal energy to do work, such as a combustion engine, are known as heat engines.  Heat engines are still governed by the First Law of Thermodynamics, so any exhaust heat must have been thermal energy that was not used to do work. The thermal energy input that can be used to do work rather than wasted as exhaust heat determines the efficiency of the heat engine.

Body Efficiency

The efficiency of the human body in converting chemical potential energy into useful work is known as the mechanical efficiency of the body.  We often calculate the body’s mechanical efficiency, as a percentage:

(2)   \begin{equation*} e_{body} = \frac{W_{by}}{Chemical\, Potential\, Energy\, Used}\times 100\,\bold{\%} \end{equation*}

The mechanical efficiency of the body is limited because energy used for metabolic processes cannot be used to do useful work. Additional  thermal energy generated during the chemical reactions that power muscle contractions along with friction in joints and other tissues reduces the efficiency of humans even further.[2].

Reinforcement Exercises

“Alas, our bodies are not 100 % efficient at converting food energy into mechanical output. But at about 25 % efficiency, we’re surprisingly good considering that most cars are around 20 %, and that an Iowa cornfield is only about 1.5 % efficient at converting incoming sunlight into chemical [potential energy] storage.”  [3]For an excellent discussion of human mechanical efficiency and comparisons with other machines and fuel sources, see MPG of a Human by Tom Murphy, the source of the previous quote.

Everyday Example: Energy to Climb Stairs

Assuming a 20% mechanical efficiency in climbing stairs, how much does your internal energy decrease when a 65 kg person climbs a 15 m high flight of stairs? How much thermal energy does the person transfer to the environment as exhaust heat?

First, lets calculate the change in gravitational potential energy:

    \begin{equation*} \Delta PE_g =mg\Delta h = (65\,\bold{kg}) (9.8\,\bold{m/s/s})(15\,\bold{m}) = 9,555\, \bold{J} \end{equation*}

The person did work in converting chemical potential energy in their body to mechanical energy, specifically gravitational potential energy. However, they are only 20% efficient, which means that only 1/5 of the chemical potential energy they use goes into doing useful work. Therefore the change in chemical potential energy must have been 5x greater than the mechanical work output

    \begin{equation*} Chemical\, Potential\, Energy\, Used = (5 \times 9,555\, \bold{J})= 47,775\,\bold{J} \end{equation*}

The chemical potential energy used came out of the person’s internal energy so:

    \begin{equation*} \Delta U = - 47,775 \,\bold{J} \end{equation*}

We can use the First Law of Thermodynamics to find the thermal energy exhausted by the person:

(3)   \begin{equation*} \Delta U = Q - W_{by} \end{equation*}

Rearranging for Q:

    \begin{equation*} Q = \Delta U + W_{by} = - 47,775 \,\bold{J}+ 9,555\, \bold{J} = -38,220\, \bold{J} \end{equation*}

We find that the heat is negative, which makes sense because the person exhausts thermal energy out of the body and into to the environment while climbing the stairs.

Alternatively, we could have known right off that the exhaust heat must be 4/5 of the total loss of internal energy, because only 1/5 went into doing useful work. So the exhaust heat should be:

    \begin{equation*} Q = \Delta U \times (4/5)= - 47,775 \,\bold{J} \times 4/5 = -38,220\, \bold{J} \end{equation*}

Food Calories

For historical reasons we often measure thermal energy and heat in units of calories (cal) instead of Joules.  There are 4.184 Joules per calorie. We measure chemical potential energy stored in food with units of 1000 calories, or kilocalories (kcal) and we sometimes write kilocalories as Calories (Cal) with with capital C instead of a lowercase c. For example, a bagel with 350 Cal has 350 kcal, or 350,000 cal. Converting to Joules, that would be 350,000 \,\bold{cal} times (4.184 \,\bold{J}/bold{cal}) =1,464,400\, \bold{J} in the bagel.

Everyday Examples

What fraction of a bagel would you need to eat in order to make up for the 47,775 J  loss of internal energy (as chemical potential energy) that we calculated in the previous everyday example about climbing stairs?

There are 1,464,400  J/bagel

Therefore we need to eat:

    \begin{equation*} \frac{47,775 \,\bold{J}}{1,464,400\, \bold{J}/bagel} = 0.03\, Bagels\, or\, 3\, \bold{\%}\, of \, a\, bagel \end{equation*}

Reinforcement Exercises

Conservation of Mass and of Energy

A person is measuring the amount of oxygen in blood and metabolic rate using a pulse oxymeter. The pulse oxymeter is strapped to the person’s wrist, and the index finger is inside the clip.
A pulse oxymeter is an apparatus that measures the amount of oxygen in blood. Oxymeters can be used to determine a person’s metabolic rate, which is the rate at which food energy is converted to another form. Such measurements can indicate the level of athletic conditioning as well as certain medical problems. (credit: UusiAjaja, Wikimedia Commons)

The digestive process is basically one of oxidizing food, so energy consumption is directly proportional to oxygen consumption. Therefore, we can determine the the actual energy consumed during different activities by measuring oxygen use. The following table shows the oxygen and corresponding energy consumption rates for various activities.

Energy and Oxygen Consumption Rates for an average 76 kg male
Activity Energy consumption in watts Oxygen consumption in liters O2/min
Sleeping 83 0.24
Sitting at rest 120 0.34
Standing relaxed 125 0.36
Sitting in class 210 0.60
Walking (5 km/h) 280 0.80
Cycling (13–18 km/h) 400 1.14
Shivering 425 1.21
Playing tennis 440 1.26
Swimming breaststroke 475 1.36
Ice skating (14.5 km/h) 545 1.56
Climbing stairs (116/min) 685 1.96
Cycling (21 km/h) 700 2.00
Running cross-country 740 2.12
Playing basketball 800 2.28
Cycling, professional racer 1855 5.30
Sprinting 2415 6.90

Everyday Examples: Climbing Stairs Again

In the previous examples we assumed stated that our mechanical efficiency when climbing stairs was 20%. Let’s use the data in the above table to verify that assumption. The data in the table is for a 76 kg person climbing 116 stairs per minute. Let’s calculate the rate at which that person did mechanical work while climbing stairs and compare that rate at which they used up internal energy (originally from food).

The minimum standard step height in the US is 6.0 inches[4] (0.15 m) then the gravitational potential energy of a 76 kg person will increase by 130 J with each step, as calculated below:

    \begin{equation*} \Delta PE = mg\Delta h = (76\,\bold{kg})(9.8\,\bold{m/s/s})(0.15\,\bold{m}) = 112\,\bold{J} \end{equation*}

When climbing 116 stairs per minute the rate of energy use, or power, will then be:

    \begin{equation*} P = (112\,\bold{J})\left(116\, \frac{stairs}{\bold{min}}\right)\left(\frac{1\,\bold{min}}{60\,\bold{sec}}\right) = 216 \,\bold{W} \end{equation*}

According to our data table the body uses 685 W to climb stairs at this rate. Let’s calculate the efficiency:

    \begin{equation*} e = \frac{216\,\bold{W}}{685 \,\bold{W}} = 0.32 \end{equation*}

As a percentage, this person is 32% mechanically efficient when climbing stairs. We may have underestimated in the previous examples when we assumed a 20% efficiency for stair climbing.

Reinforcement Exercises

We often talk about “burning” calories in order to lose weight,  but what does that really mean scientifically?. First, we really we mean lose mass because that is the measure of how much stuff is in our bodies and weight depends on where you are (it’s different on the moon). Second, our bodies can’t just interchange mass and energy — they aren’t the same physical quantity and don’t even have the same units. So how do we actually lose mass by exercising? We don’t actually shed the atoms and molecules that make up body tissues like fat by “burning” them. Instead, we break down the fat molecules into smaller molecules and then break bonds within those molecules to release chemical potential energy, which we eventually convert to work and exhaust heat.  The atoms and smaller molecules that resulting from breaking the bonds combine to form carbon dioxide and water vapor (CO2 and H2O) and we breath them out. We also excrete a bit as H2O in sweat and urine. The process is similar to burning wood in campfire — in the end you have much less mass of ash than you did original wood. Where did the rest of the mass go? Into the air as CO2 and H2O. The same is true for the fuel burned by your car. For more on this concept see the first video below. The really amazing fact is that your body completes this chemical process without the excessive temperatures associated with burning wood or fuel, which would damage your tissues. The body’s trick is to use enzymes, which are highly specialized molecules that act as catalysts to improve the speed and efficiency of chemical reactions, as described and animated in the beginning of the second video below.

 

General Efficiency

Similar to the body efficiency, the efficiency of any energetic process can be described as the amount of energy converted from the input form to the desired form divided by the original input amount. The following chart outlines the efficiencies of various systems at converting energy various forms. The chart does not account for the cost, hazard risk, or environmental impact associated with the required fuel, construction, maintenance, and by-products of each system.

The Efficiency of the Human Body Compared to Other Systems
System Input Energy Form Desired Output Form Max Efficiency
Human Body Chemical Potential Mechanical 25 %
Automobile Engine Chemical Potential Mechanical 25 %
Coal/Oil/Gas Fired Stream Turbine Power Plants Chemical Potential Electrical 47%
Combined Cycle Gas  Power Plants Chemical Potential Electrical 58 %
Biomass/Biogas Kinetic Electrical 40%
Nuclear Kinetic Electrical 36%
Solar-Photovoltaic Power Plant Sunlight (Electromagnetic) Electrical 15%
Solar-Thermal Power Plant Sunlight (Electromagnetic) Electrical 23%
Hydroelectric and Tidal Power Plants Gravitational Potential Electrical 90%+

[5][6][7]

Check out the energy systems tab in this simulation to visualize different energy conversion systems

Energy Forms and Changes

  1. Significant content in this chapter was adapted from: OpenStax, College Physics. OpenStax CNX. Aug 30, 2019 http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@17.22 ↵
  2. "The maximum work and mechanical efficiency of human muscles, and their most economical speed" by A. V. Hill,National Library of Medicine, U.S. National institutes of Health ↵
  3. "MPG of a Human" by Tom Murphy, Do The Math, UCSD Physics Department ↵
  4. "1917.120 - Fixed stairways." by Occupational Safety and Health Administration, United States Department of Labor ↵
  5. "Managing Water in the West: Hydroelectric Power" by Bureau of Reclimation, U.S. Department of the Interior ↵
  6. "Efficiency in Electricity Generation" by EURELECTRIC “Preservation of Resources” Working Group’s “Upstream” Sub-Group in collaboration with VGB, Union of the Electricity Industry ↵
  7. "Efficiency of Energy Conversion Devices" by John E. Dutton e-Education Institute, Penn State College of Earth and Mineral Sciences ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Body Physics: Motion to Metabolism Copyright © by Lawrence Davis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book