Tipping

Lawrence Davis

42 Tipping

Torque

When you hold an object in your hand, the of the object tends to cause a rotation of the forearm with the elbow joint acting as the . The force applied by your biceps tries to counteract this rotation.

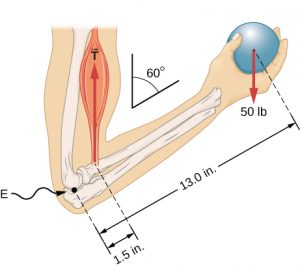
Figure is a schematic drawing of a forearm rotated around the elbow. A 50 pound ball is held in the palm. The distance between the elbow and the ball is 13 inches. The distance between the elbow and the biceps muscle, which causes a torque around the elbow, is 1.5 inches. Forearm forms a 60 degree angle with the upper arm. — The elbow joint flexed to form a 60° angle between the upper arm and forearm while the hand holds a 50 lb ball. The weight of the ball exerts a torque on the forearm *about* the elbow joint. Image Credit: Openstax University Physics

^[1]

When forces applied to an object tend to cause rotation of the object, we say the force is causing a . The size of a torque depends on the size of the , the direction of the force, and the distance from the point to where the force acts.

Reinforcement Activity

Static Equilibrium

In order for an object to remain still then any torques cancel each other out so that there is no . If the net torque is not zero the the object will begin to rotate rather than remain still. For example, in our example of the forearm holding the ball, the torque due to biceps and torque due to ball must be equal, but in opposite directions.

Reinforcement Exercises

Tipping Point

When a body’s is above the area formed by the the can provide the necessary to remain in .

A box sits with its bottom flush against sloping ground. An arrow labeled normal force points upward from bottom of the box on the uphill side. An arrow labeled force of gravity points downward from the center of the box. The downhill bottom corner of the box is labeled as pivot. A rightward curved arrow is labeled torque due to normal force. An equal size, but oppositely curved arrow is labeled torque due to gravity. — An object in rotational equilibrium. The torque from normal force cancels the torque from gravity. In this case friction (not shown) acts on the bottom surface of the object to keep it from sliding downhill.

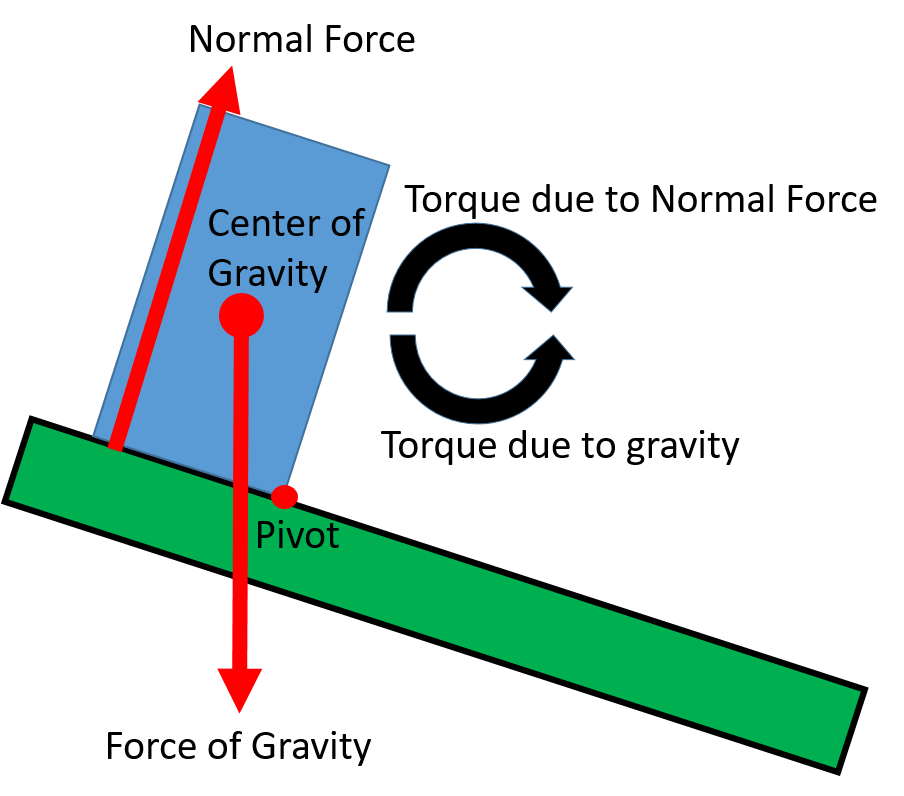
The critical is reached when the passes outside of the . Beyond the tipping point, causes rotation away from the support base, so there is no available to cause the needed to cancel out the torque caused by gravity. The normal force acting on the point can help support the object’s weight, but it can’t create a because it’s not applied at any distance away from the pivot.

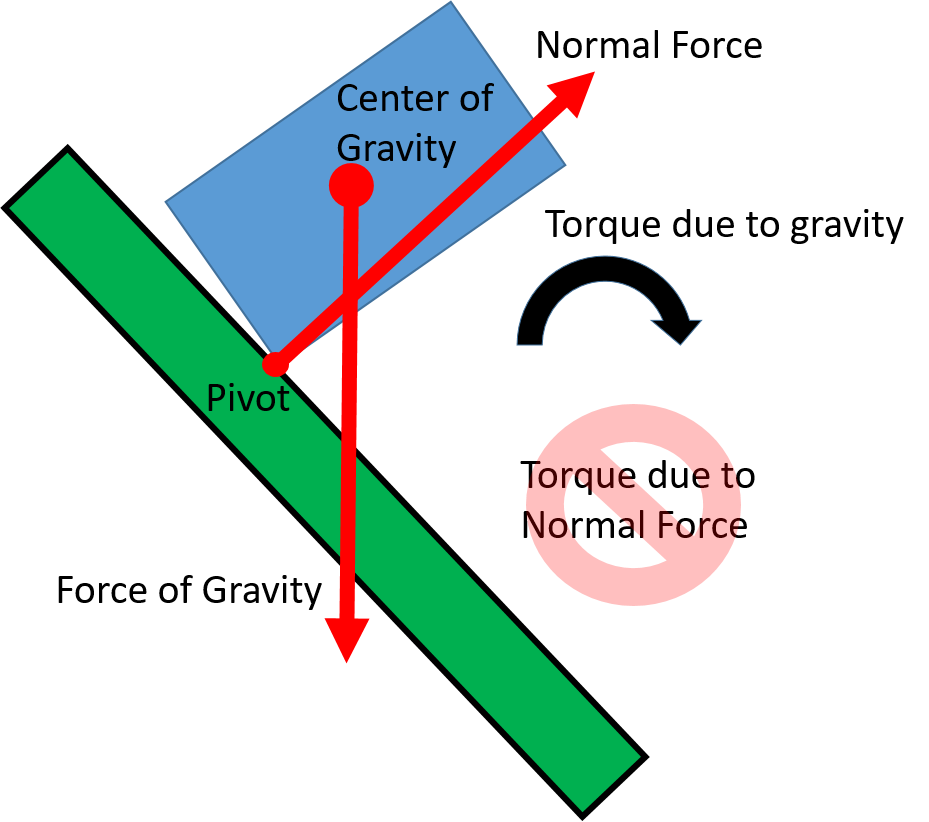
A box is in the process of tipping over on sloping ground. An arrow labeled force of gravity points downward from the center of the box. The downhill bottom corner of the box is labeled as pivot. An arrow labeled normal force points upward from the pivot. A rightward curved arrow is labeled torque due to gravity. Torque due to normal force is slashed through to indicate its absence. — An object out of rotational equilibrium. The normal force acting at the pivot cannot produce a torque to cancel the torque caused by gravity. In this case friction (not shown) acts at the pivot point to keep the object from sliding downhill.

Now with a the object can not be in . The object will rotate around the edge of the and tip over. We often refer to structures (and bodies) that are relatively resistant to tipping over as having greater stability.

OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Jul 11, 2018 http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@10.18. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License