We started the previous unit with a discussion of Jolene’s motion during a shift on the medical floor of a hospital, including all the starts and stops that she makes. When Jolene is standing still she has zero kinetic energy. As she takes a step to begin walking she now has kinetic energy. Jolene had to supply that energy from within herself. When Jolene comes to a stop her kinetic energy is transferred to thermal energy by friction. When she begins walking again she will need to supply the new kinetic energy all over again. Even if Jolene walks continuously, every step she takes involves two inelastic collisions (the push-off and the landing) so kinetic energy is constantly being transferred to thermal energy. To stay in motion Jolene has to re-supply that kinetic energy. Walking around all shift uses up Jolene’s stored energy and that is why she gets tired.

Work

The amount of energy transferred from one form to another and/or one object to another is called the work.  Doing work is the act of transferring that energy. Doing work requires applying a force over some distance. The sign of the work done on an object determines if energy is transferred in or out of the object. For example, the athlete on the right is doing positive work on the pole because he is applying a force in the same direction as the pole’s motion. That will tend to speed up the pole and increase the kinetic energy of the pole. The athlete on the left is doing negative work on the pole because the force he applies tends to decrease the energy of the pole.

^[1]

The positive or negative sign of the work refers to energy transferring in or out of an object rather than to opposite directions in space so work is not a vector and we will not make it bold in equations.

Calculating Work

The actual amount of work done is calculated from a combination of the average force and the distance over which it is applied, and the angle between the two:

(1)  

The in the work equation automatically tells us whether the work is transferring energy into or out of a particular object:

1. A force applied to an object in the opposite direction to its motion will tend to slow it down, and thus would transfer kinetic energy out of the object. With energy leaving the object, the work done on the object should be negative. The angle between the object’s motion and the force in such a case is 180° and 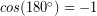, so that checks out.
2. A force applied to an object in the same direction to its motion will tend to cause it to speed up, and thus would transfer kinetic energy in to the object. With energy entering the object, the work done on the object should be positive. The angle between the object’s motion and the force in such a case is 0° and 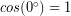so that also checks out.
3. Finally, if a force acts perpendicular to an objects motion it can only change its direction of motion, but won’t cause it to speed up or slow down, so the kinetic energy doesn’t change. That type of force should do zero work. The angle between the object’s motion and the force in such a case is 90° and 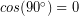so once again, the 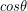in the work equation gives the required result. For more on this particular type of situation read the chapter on weightlessness at the end of this unit.

The work equation gives the correct work done by a force, no matter the angle between the direction of force and the direction of motion, even if the force points off at some angle other than 0°, 90°, or 180°. In such a case, some part of the force will be doing work and some part won’t, but the tells us just how much of the force vector is contributing to work.