77 Crumple Zones
Kinetic Energy
Crumple zones built into modern cars also serve the purpose of reducing force by increasing the collision time and minimizing bounce. Crumple zones cause cars to be totaled more often, but cars can be replaced and people can’t be. Notice that the presenter in the previous video isn’t talking about or , but he does keep mentioning absorbing . This energy that he is claiming will be absorbed by the crumple zone is the energy stored in the motion of the car. Any moving object has this type of energy, known as (KE). The amount of kinetic energy an object has depends on its and its :
(1) 
Notice that the depends on , but not because KE doesn’t have a direction (an object can’t have negative KE). Even if we input a negative velocity into the KE equation, it gets squared so KE would come out positive anyway. The unit of kinetic energy is a Nm, which has it own name, the (J).
Reinforcement Activity
Elastic Potential Energy
During the collision the car materials were compressed by the wall. If the stress remained below the of the materials, so they were remained in the , then the kinetic energy from the car would have been transferred into elastic stored in the of the materials. This stored energy has the potential to become kinetic energy, which is exactly what would happens when the materials then spring back causing the car to “bounce” back from the wall.
Reinforcement Exercise
If the car had bounced back at the same that it had entering the collision, then the final would be the same as the initial, and we would say that kinetic energy had been . Collisions that conserve kinetic energy are known as . Collisions that don’t are known as . In the previous chapter we learned that bounce was bad when it comes to minimizing the force on the body during a collision. The purpose of crumple zones is to ensure that very little of the kinetic energy remains after the collision by making them very inelastic. The key to accomplishing that is to ensure that kinetic energy is transferred into thermal energy instead of elastic potential energy by designing the materials to break instead of bounce.
Thermal Energy
If you watch the video carefully, you see that the car was moving forward, then for a moment it was stopped and thus had zero , and then it was moving backward (though not as fast), so once again it had kinetic energy. Some of the original kinetic energy was stored as elastic potential energy and then released as kinetic energy again, but most of it was not. If you are wondering where that energy went, then you are was very perceptive, because in fact the tells us that energy cannot be created or destroyed, only transferred from one form to another and/or one object to another, via .
The applied to the materials during the collision caused a on the materials. Some materials were stressed above their so they . Some other materials didn’t fracture, but were stressed beyond their and into their so that they were permanently deformed. In either case, the done to deform the materials transferred into , effectively slowing the car down, but warming it up. Crumple zones are designed to deform permanently in order to convert kinetic energy into thermal energy.
Reinforcement Exercises
Microscopic Kinetic Energy
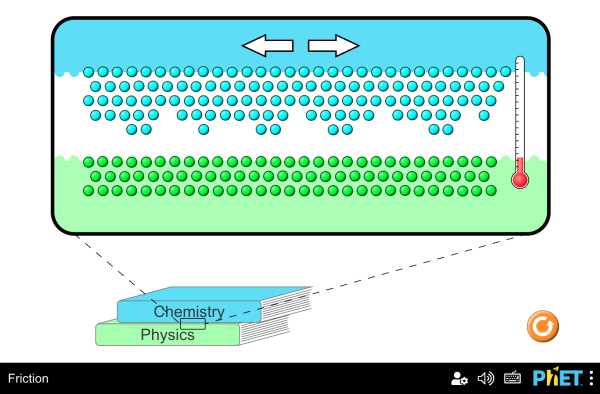
Now that we have introduced as a new type of , we will reverse course and say that thermal energy is not actually a new type of energy, but rather just on a microscopic scale. Thermal energy is the energy stored in the motion of atoms and molecules that make up a material. Transferring thermal energy to a system really just means that you caused it’s atoms and molecules to move faster. The work done in compressing objects past their and the work done by will always transfer some energy into thermal energy. You can visualize this microscopic process for kinetic friction using the simulation below.
Coefficient of Restitution
The relative elasticity of collisions is defined by the (COR) which relates the final kinetic energy and the initial kinetic energy. For a moving object striking a stationary object that doesn’t move, as in the crumple zone video, the COR is calculated as final divided by initial speed.
(2) 
A would have a COR of one. If any materials are permanently deformed during a collision then you can be sure the collision was not perfectly elastic. In fact, perfectly elastic collisions don’t really occur, but many situations come very close and we can approximate them as perfectly elastic.
Check out this simulation that allows you to visualize different types of collisions.
the average force applied during a time interval multiplied by the time interval
the combined effect of mass and velocity, defined as mass multiplied by velocity
A quantity representing the capacity of an object or system to do work.
energy which a body possesses by virtue of being in motion, energy stored by an object in motion
a measurement of the amount of matter in an object made by determining its resistance to changes in motion (inertial mass) or the force of gravity applied to it by another known mass from a known distance (gravitational mass). The gravitational mass and an inertial mass appear equal.
distance traveled per unit time
a quantity of speed with a defined direction, the change in speed per unit time, the slope of the position vs. time graph
a system of physical units ( SI units ) based on the meter, kilogram, second, ampere, kelvin, candela, and mole
International standard (SI) unit of Energy
the value of the stress (yield stress) and strain (yield strain) beyond which a material will maintain some permanent deformation
the range of values for stress and strain values over which a material returns to its original shape after deformation
the energy stored within an object, due to the object's position, arrangement or state. Examples are gravitational potential energy due to the relative position of masses and elastic potential energy caused by being under stress
reduction in size caused by application of compressive forces (opposing forces applied inward to the object).
a physical quantity is said to be conserved when its total value does not change
a collision for which initial and final values of the total kinetic energy of all objects in the system are the same
a collision for which kinetic energy is not conserved
Energy cannot be created or destroyed, only transferred from one type to another and/or from one object to another
A quantity representing the effect of applying a force to an object or system while it moves some distance.
any interaction that causes objects with mass to change speed and/or direction of motion, except when balanced by other forces. We experience forces as pushes and pulls.
a physical quantity that expresses the internal forces that neighboring particles of material exert on each other
the maximum stress a material can withstand
the separation of an object or material into two or more pieces under the action of stress and associated strain
the maximum stress that can be applied to a material before it leaves the linear region
the range of values for stress and strain over which a material experiences permanent deformation
energy stored in the microscopic motion of atoms and molecules (microscopic kinetic energy)
a force that resists the sliding motion between two surfaces
the fraction of relative velocity remaining after a collision, for collision with a stationary object equal to the ratio of final speed to initial speed
