Ultimate Strength of the Human Femur

Lawrence Davis

51 Ultimate Strength of the Human Femur

Compressing the Femur

Opposite to tension forces, compression forces are provided by a material in response to being compressed rather than stretched. The resistance of materials to deformation is what causes the normal force (support force) that we introduced in the unit on balance. For example, the femur is compressed while supporting the upper body weight of a person.

The Human Femur. Image Credit: Anatomography via Wikimedia Commons

^[1]

“In human anatomy, the femur (thigh bone) is the longest and largest bone. Along with the temporal bone of the skull, it is one of the two strongest bones in the body. The average adult male femur is 48 cm (18.9 in) in length and 2.34 cm (0.92 in) in diameter and can support up to 30 times the weight of an adult.”^[2]The average weight among adult males in the United States is 196 lbs (872 N)^[3]. According to the statement that the femur can support 30x body weight, the adult male femur can support roughly 6,000 lbs of compressive force! Such high forces are rarely generated by the body under its own power, thus motor vehicle collisions are the number one cause of femur fractures^[4].

Stress

The size of object affects how they deform in response to applied compression and tension forces. For example, the maximum compression or tension forces that a bone can support depends on the size of the bone. More specifically, the more area available for the force to be spread out over, the more force the bone can support. That means the maximum forces bones, (and other objects) can handle are proportional to the cross-sectional area of the bone that is perpendicular (90°) to the direction of the force. For example, the force that the femur can support vertically along its length depends on the area of its horizontal cross-sectional area which is roughly circular and somewhat hollow (bone marrow fills the center space).

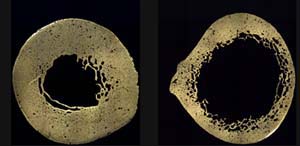
The femur cross-section on right shows significant reduction in bone thickness and reduced density near the inner surface. — These cross sections show the midshaft of the femur of an 84-year-old female with advanced osteoporosis (right), compared to a healthy femur of a 17-year-old female (left). Image Credit: Smithsonian National Museum of Natural History

^[5]

Larger bones and tendons can support more force, so in order to analyze the behavior of the bone material itself we would need to divide the force applied to by the cross-sectional area ( $A_x$ ). The resulting quantity is known as the stress (σ) on the material. Stress has units of force per area so the SI units are (N/m²) which are also known as Pascals. Units of pounds per square inch (PSI, lbs/in²) are common in the U.S.

(1) $\begin{equation*} stress = \sigma = \frac{F}{A_x} \end{equation*}$

Reinforcement Exercises

Ultimate Strength of the Femur

The maximum stress that bone, or any other material, can experience before the material begins fracture or rupture is called the ultimate strength. Notice that material strength is defined in terms of stress, not force, so that we are analyzing the material itself, without including the effect of how much material is present. For some materials the ultimate strength is different when the stress is acting to crush the material (compression) versus when the forces are acting to stretch the material under tension, so we often refer to ultimate tensile strength or ultimate compressive strength. For example, the ultimate compressive strength for human femur bone is measured to be 205 MPa (205 Million Pascals) under compression along its length. The ultimate tensile strength of femur bone under tension along its length is 135 MPa.^[6] Along with bone, concrete and chalk are other examples of materials with different compressive and tensile ultimate strengths.

Reinforcement activity

Everyday Example: Femur Ultimate Strength

Let’s check to see if the measured values for compressive ultimate strength agree with the claim that the human femur can support 30x the adult body weight, or roughly 6,000 lbs

First let’s to convert the claimed 6,000 lbs force to Newtons and work in SI units.

$\begin{equation*} 6,000\, \bold{lbs} = 6,000\, \cancel{\bold{lbs}} \left(\frac{4.45\, \bold{N}}{1\, \cancel{\bold{lb}}}\right) = 26,166 \bold{N}. \end{equation*}$

An approximate minimum cross-sectional area of the femur is $3.2\times 10^{-4}\, \bold{m^2}$ . (*See the bottom of this example if you are interested in learning how we approximated this value). We divide the compressive force by the cross-sectional area to find the compressive stress on the bone.

$\begin{equation*} Stress = \frac{force}{area} = \frac{26,166\, \bold{N}}{3.2\times 10^{-4}\, \bold{m^2}} = 80,000,000\, \bold{Pa} = 80\, \bold{MPa} \end{equation*}$

Our approximate value for the ultimate strength of bone that would be required to support 30x body weight was 80 MPa, which is actually less than the measured value of 205 MPa, so the claim that the femur can support 30x body weight seems reasonable.

*This is how we approximated the femur cross-sectional area, skip this if you aren’t interested:

First we divide the 2.34 cm femur diameter quoted earlier by two to find the femur radius, then we convert to standard units of meters.

$\begin{equation*} r = \frac{2.34\, \cancel{\bold{cm}}}{2}\left(\frac{1\, \bold{m}}{100\, \cancel{\bold{cm}}}\right) = 0.0117\, \bold{m} = 1.17 \times 10^{-2} \end{equation*}$

Using the equation for the area of a circle we calculate the total area of the femur to be:

$\begin{equation*} A_{out} = \pi r^2 = \pi \left(0.0117\, \bold{m}\right)^2 = 0.00043\, \bold{m^2} = 4.3 \times 10^{-4}\, \bold{m^2} \end{equation*}$

Finally we have to subtract off the area of the hollow middle part to get the net bone area. We used a ruler on the above picture of the femur cross-sections to see that the inner radius is roughly half of the outer radius, or $5.85\, \times 10^{-3} \bold{m}$ so we calculate the missing inner area:

$\begin{equation*} A_{in} = \pi r^2 = \pi \left(5.85 \times 10^{-3}\, \bold{m}\right)^2 = 1.1 \times 10^{-4}\, \bold{m^2} \end{equation*}$

And subtract off the inner area from the total:

$\begin{equation*} A_{x} = 4.3 \times 10^{-4}\, \bold{m^2} -1.1 \times 10^{-4}\, \bold{m^2} = 3.2\times 10^{-4}\, \bold{m^2} \end{equation*}$

Transverse Ultimate Strength

So far we have discussed ultimate strengths along the long axis of the femur, known as the longitudinal direction. Some materials, such as bone and wood, have different ultimate strengths along different axes. The ultimate compressive strength for bone along the short axis (transverse direction) is 131 MPa, or about 36% less than the 205 MPa longitudinal value. Materials that have different properties along different axes are known as anisotropic. Materials that behave the same in all directions are called isotropic.

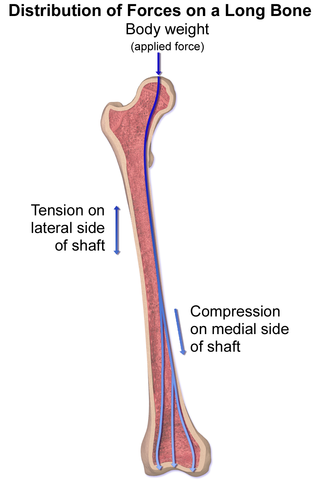
An interesting fact to finish up this chapter: when a person stands the femur actually experiences compressive and tensile stresses on different sides of the bone. This occurs because the structure of the hip socket applies the load of the body weight off to the side rather than directly along the long axis of the bone.