102 Unit 4 Lab: Hydrostatic Weighing (Distance Learning Compatible)
Comparing Methods of Density Measurement
This lab is designed to align with AAOT science outcome #1: Gather, comprehend, and communicate scientific and technical information in order to explore ideas, models, and solutions and generate further questions.
Materials
- writing utensil
- calculator
- digital device with spreadsheet program
- digital device with internet access
ObjectiveS
- Determine the volume of an object using the displacement method.
- Calculate the density of an object from mass and volume.
- Apply Archimedes’ Principle to determine the density of an object from measurements of weight and apparent weight.
- Compare and contrast various methods for determining density.
- Understand how hydrostatic weighing and empirical models are used to estimate body fat percentage.
Experimental Methods
We will determine the density of a potato using mass found from a scale and volume found two different ways and then compare those results. Finally we will determined using hydrostatic weighing, which does not require a direct volume measurement and compare those results as well. The following video shows the necessary data being collected.
Approximate Sphere Method
Data Acquisition
[Outcome 4-1]
1) Record the potato mass provided by the scale (in units of grams):__________g
2) Record the potato circumference (in units of cm): __________cm
3) Look up a formula that relates the volume of a sphere to it’s circumference. Record the formula below and cite your source (provide a citation that includes a full URL, not just a website name.)
Data Analysis
4) Model the potato as a sphere to estimate the volume of the potato and be sure to include correct units in your answer. Show your work.
5) Use the mass and volume to calculate the potato density, be sure to include correct units in your answer. (You may need to look up how density is defined by mass and volume.) Cite your source and show your work.
Displacement Method
[Outcome 4-1]
Data Acquisition
6) Record the volume of water displaced by the potato when fully submerged:___________ cm3. Assuming there are no trapped air bubbles, the fully submerged displaced volume is same as the volume of the potato.
Data Analysis
[Outcome 4-4]
7) Calculate the potato density from the mass reading on the scale and the volume determined by displacement. Show your work.
8) How do the results from the previous two methods of determining density compare? Calculate a % difference between the two results. Show your work.
Conclusions
9) Which result do you trust more? Explain your reasoning in detail. [Hint: Your reasoning should involve a comparison of the sources and sizes uncertainties in the measurements used for each method.]
Hydrostatic Method
The hydrostatic method allows us to reduce uncertainty in measuring the density of objects with complex shapes by eliminating the need for a direct volume measurement. Instead we apply Archimedes’ Principle and the concept of static equilibrium to calculate the volume from measurements of the weight and apparent weight.
10) Record the weight of the potato in air (use units of Newtons) :___________N
11) Record the weight of the fully submerged potato here:___________N. This is known as the the apparent weight because the object appears to weigh less when it is submerged. In hydrostatic weighing applications, the apparent weight is sometimes called the under-water weight.
12) Based on your measured weight and apparent weight, what must be the size of the buoyant force that pushes up on the submerged potato? [Hint: The object is not moving, so it must be in static equilibrium. Draw a free body diagram of the potato to help you answer this question, but don’t forget to include the upward force from the hook attached to the scale].
13) Write Archimedes principle. [Hint: It tells you how the buoyant force on an object relates to the weight of fluid displaced by the object.]
14) You have already found the buoyant force using static equilibrium, so now apply Archimedes principle to find the weight of the water displaced by the object. Explain. Your reasoning.
15) Use the weight of the displaced water to calculate the mass of the water displaced. Show your work.[Hint: How are mass and weight related for an object near the surface of the Earth?]
16) Convert your mass to grams:
17) Look up the density of water in units of g/cm3 and record here:________
19) Now use the density of water you looked up and the mass of the water displaced by the object to find the volume of the water displaced by the object. You may need to rearrange the density formula. Show your work.
You have now found the volume of water that was displaced by the fully submerged potato, and therefore the volume of the potato. Notice that with the hydrostatic method we found the volume of the potato from measurements of weight and apparent weight and the known water density, but we didn’t attempt to measure the potato volume directly. Now you know the volume of the potato, so you just need to know its mass to calculate it’s density.
20) Use the weight that you found at the start of the hydrostatic method to calculate the mass in kg. [Hint: How are mass and weight related for an object near the surface of the Earth?]
21) Convert the potato mass you found above to grams.
22) Now use the the above potato mass (in g) and volume in (in cm3) to calculate the potato density. Show your work.
Conclusions
23) How do the results from the hydrostatic method and other two methods compare? Calculate a % difference between each set of results. Show your work.
24) Which result do you trust more? Explain your reasoning in detail. [Hint: Your reasoning should involve a comparison of the sources and sizes uncertainties in the measurements used for each method.]
Further Questions
Even for objects with complex shapes we can measure mass on a scale and finding volume from a displacement measurement, like we did in the second experiment (displacement method). Does the hydrostatic method allow any real advantages over the displacement method?
Determination of body density for the purpose of estimating body fat percentage is an example of the usefulness of the hydrostatic method. The following video illustrates the procedure.
To determine the density of a person by instead finding their volume the displacement method, you would need to submerge them, have them expel the air from their lungs, and the wait while the surface of the water settled down so that you could mark it and measure the displacement. Notice how much the surface is moving due to the bubbles and movement of the person. Spread out over the entire water surface, even a half centimeter error in measuring water line would add significant error to the volume measurement.
25) If the tub is 100 cm wide by 150cm long, similar to the one in the video, what volume error would result from a 0.5 cm error in the water line?
The hydrostatic method eliminates uncertainty associated with the water line measurement, but not the uncertainty associated with estimating the residual lung volume, which would also need be done with the displacement method. For people, residual volume can be estimated from empirical models that depend on age, height, and gender, as seen in the diagram below. Once density is determined from the hydrostatic method, using an empirical model that requires body density, ![]() , as an input. The model looks like this (using under water weight to mean the same thing as apparent weight).
, as an input. The model looks like this (using under water weight to mean the same thing as apparent weight).
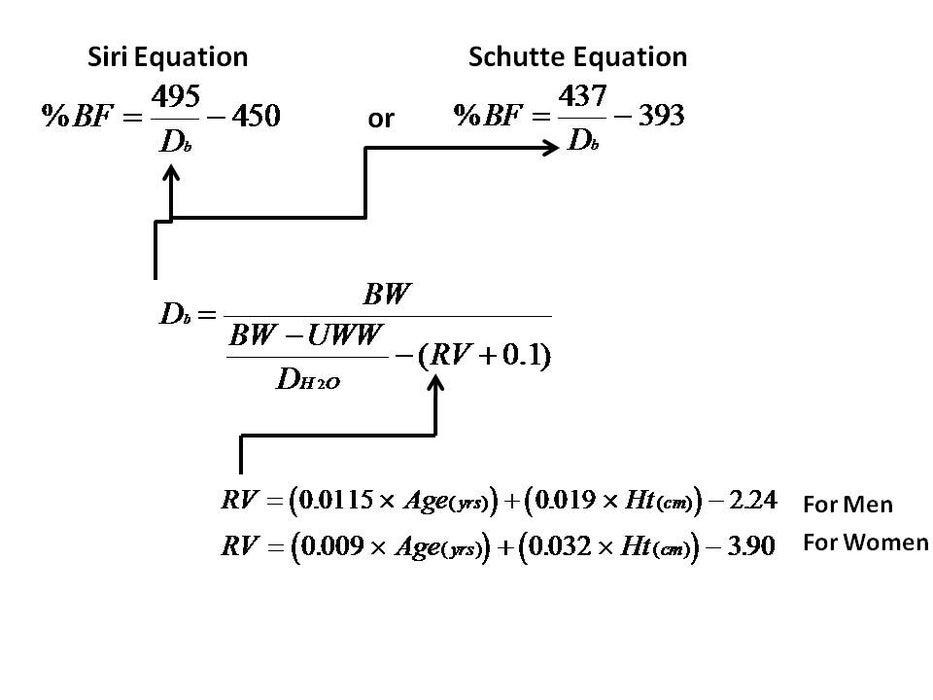
The work you did in the hydrostatic weighing part of this lab was a stepwise recreation of the equation for calculating body density ![]() that is shown in the diagram above, except for the part about residual volume of body gasses (
that is shown in the diagram above, except for the part about residual volume of body gasses (![]() ) because our potato didn’t have lungs or intestines.
) because our potato didn’t have lungs or intestines.
26) For fun we will use the potato density we found using the hydrostatic method as an input to calculate the “body fat percentage” of our potato, just as we would for a person. Follow through with that calculation of body fat percentage using the Siri Equation seen in the above diagram. Use the density value you found in units of grams/cm3. Show your work.
29) Is the BF% value your found meaningful? Explain.
Be careful when applying any model to a system it wasn’t meant to describe (a model for humans applied to a potato). Just because it will give you a result, that doesn’t mean the result is meaningful!
mathematical explanation of the relation between measured values that is used for making predictions

