12 Scientific Models
Physical and Empirical Models
A model is a representation of something that is often too difficult (or impossible) to observe or display directly. Although a model is justified by experimental tests, it is only accurate in describing certain aspects of a physical system. For example, a basic model of color vision which accounts for the response of the eye to different colors, but not for the processing of that information by the brain[1]Such a model is not all-encompassing, but it is still useful in many situations, such as designing digital displays or creating a computer simulation to predict the results of various color combinations. Check out this interactive simulation of color vision.
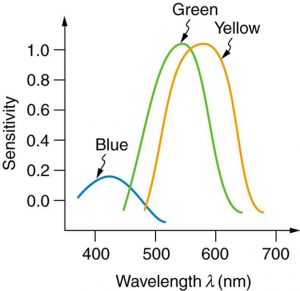
Widely applicable Physical models (mechanistic models) that explain how a system works, like the color vision model, can become theories after a preponderance of evidence has been built supporting their validity. Empirical models, which use mathematical trends in observed data, cannot become theories, but they are still useful for making decisions once they have sufficiently been validated.
Qualitative and Quantitative Models
Both physical and empirical models can be either qualitative or quantitative. Qualitative models predict what behavior you expect to observe, while quantitative models predict behaviors to observe and actual values of measurements. The following table will help you understand the different types of models. The amount of information provided by the model increases as you move from upper left to lower right of the table.
| Empirical | Physical (Mechanistic) | |
| Qualitative | In the absences of air resistance, objects dropped from the same height will hit the ground at the same time, no matter what the objects are. | When you drop something it falls due to mutual gravitational attraction with the Earth. More massive things feel a greater attraction, but they are also more difficult to accelerate, so everything ends up accelerating at the same rate. |
| Quantitative | Without air resistance, everything falls with the same acceleration value of 9.8 m/s/s. | Combining Newton’s Law of Universal Gravitation and Newton’s 2nd Law of Motion, to predict that the free-fall acceleration for objects at the surface of the Earth should be 9.8 m/s/s. (And it is!). |
Stay tuned, the Unit 2 lab will produce a quantitative empirical model for the fall time of certain objects from a certain height when air resistance is present.
Computer Models
Computer modeling is a relatively new tool for science, but it still fits right into the overall process. Computer models are often used to assist in making predictions to be tested experimentally. Sometimes computer models are used as surrogates for expensive, time consuming, or complex, experiments to inform the experimental design process. However computer models are not permanent substitutes for experimentation and the results of computer models should be verified by experimentation or observational data. Computer models which have been verified against data are exceptionally helpful in making predictions used in decision making. For example modeling high altitude winds to plan airliner flight paths and modeling storm paths to plan emergency procedures.
Reinforcement Exercises
- [1] OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Jun 5, 2018http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@10.16. ↵
a representation of something that is often too difficult (or impossible) to observe or display directly
mechanistic explanation of how a physical system works
mathematical explanation of the relation between measured values that is used for making predictions
describing what happens, but not how much happens
describing what and how much happens
using a computer program that is designed to simulate what might or what did happen in a situation

