Everyday Examples: Responding to a Code Without Slipping

Jolene is walking with a speed of a 2.5 mph down the hospital corridor when a code is called over the intercom. She stops then turns around and starts walking the other direction, toward the room where the code was called, at a speed of 4.0 mph.  If Jolene’s mass is 61 kg and she tried to make that move very quickly, in only 0.75 s, for example, what net force would be applied to her?

We have only been given speeds in the problem, but in order to analyze velocity we need to define direction of motion. Let’s assign Jolene’s initial direction as the negative direction so her initial velocity was -2.5 mph. In that case her final velocity was +4.2 mph. We can calculate her change in velocity as:

(1)  

If we convert our answer to units of m/s we get: 6.5 mph = 2.9 m/s. (You can check this yourself using unit analysis or an online unit converter).

Next we calculate  Jolene’s acceleration using the definition of average acceleration:

Entering our values:

We find that Jolene’s acceleration is  3.9 m/s/s, which means that her velocity becomes 3.9 m/s more positive each second. Notice that she was originally moving in the negative direction, so having a velocity that is becoming more positive means that she must have slowed down.

Now we can use Newton’s Second Law to calculate the average net force required to provide this acceleration:

We are now ready to enter our values:

Friction is the only horizontal force contributing to the horizontal acceleration Jolene experiences, so the net force would just be equal to the friction force. We can figure out if Jolene would slip by comparing the required net force  to the maximum possible static friction force.

First we start with the equation for max static friction force:

Then we divide by the normal force to solve for the friction coefficient:

Assuming the floor is level and only Jolene’s horizontal motion is changing, then the normal force must be balancing Jolene’s weight (if these were not balanced then she would have a vertical acceleration as well). For this special case we substitute her weight for the normal force:

Finally we enter our values:

Looking up friction coefficients we find that the rubber-concrete friction coefficient is typically 0.6 or greater, so Jolene could likely make this move without slipping.

Everyday Example: Jumping

When a person stands still on flat ground, they are in static equilibrium and the normal force pushing up from the ground is equal to their weight. In order to jump, the muscles of the leg contract to push down against the floor. This downward push results in an equal reactive normal force from the floor, so that now the normal force is greater than body weight a there is an upward net force. Now with an upward net force, the body will experience an upward acceleration. The following graph of the normal force on person was created by jumping and landing on a force plate, which is essentially a extra-tough digital scale that records the normal force that it provides over time.

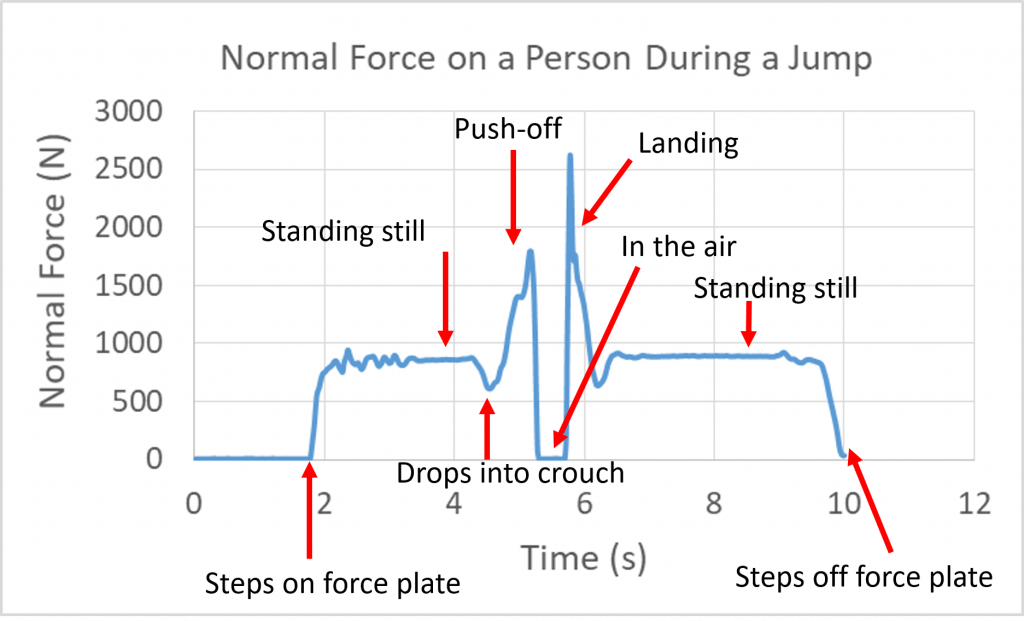
First the jumper steps on the force plate and it reads their weight of about 800 N. Then the plate reading dips a couple hundred Newtons because the upward normal force is reduced as they drop down into a crouch, which makes sense because they must accelerate downward to drop down. Next the force peaks to near 1700 N they push off hard to stop their downward motion and initiate upward motion. Throughout this stage the normal force is greater than the weight in order to create this upward acceleration. The normal force drops to zero as the body leaves contact with the ground. While in the air gravity provides the net downward force so the acceleration is downward,  and the body’s upward velocity slows. (After leaving the ground the acceleration is –g= –9.8 m/s/s). The body eventually turns around as the upward velocity reaches zero, and then begins to move back toward the ground. Landing requires an upward acceleration to stop the downward velocity, so a large upward normal force of over 2500 N is produced. The jumper is attempting a “soft landing” and so continues into a crouching position during landing, which causes another couple hundred Newton dip in the normal force at the end of landing. Finally, the normal force equals weight again after landing is complete. Upcoming chapters will talk more about “soft landings” and other methods of injury prevention.

Everyday Example: Driving

In order for your car to accelerate along a flat road, it must have a net horizontal force. What force acts on your car to provide this net force? Remember the force must be on the car from another object, the car can’t put a net force on itself (so the answer can’t be the engine or any part of the car). Gravity and normal force are external forces on a car, but those forces act vertically and cannot contribute to a horizontal acceleration. The force that acts on your car in the horizontal direction is friction. When the tires attempt to rotate, they push against the ground via friction, and the ground pushes back with an equal  reactionary friction force, according to Newton's Third Law. Then, according to Newton's Second Law, that friction force acting on the car causes it to accelerate. The purpose of the throttle, engine, and drive train is to cause the tires to push back on the road in order to receive the forward push from the road in return.

^[1]

Also, your car pushes on the air to move it out the way, so according to Newton's 3rd Law, the air puts a drag force  back on your car. When  the drag force and the friction force on the car are equal the car reaches a constant velocity, sort of like terminal velocity. If you want the car to go faster, you need to increase the friction force on the car from the road,  which you achieve by increasing how hard the tires push against the road via the throttle, engine, and drive train successively.

Every Day Examples: Walking and Running

When walking or running you push horizontally against the floor and the floor pushes back, providing you with the net force necessary to create acceleration. Walking at constant average speed is achieved by alternating of forward acceleration caused when the floor pushes forward on your back foot, and backward acceleration caused by the floor pushing back on your front foot. These accelerations average out to zero so velocity appears constant, but if you use a sensor capable of taking several measurements per second,  then you can see the oscillatory nature of walking motion:

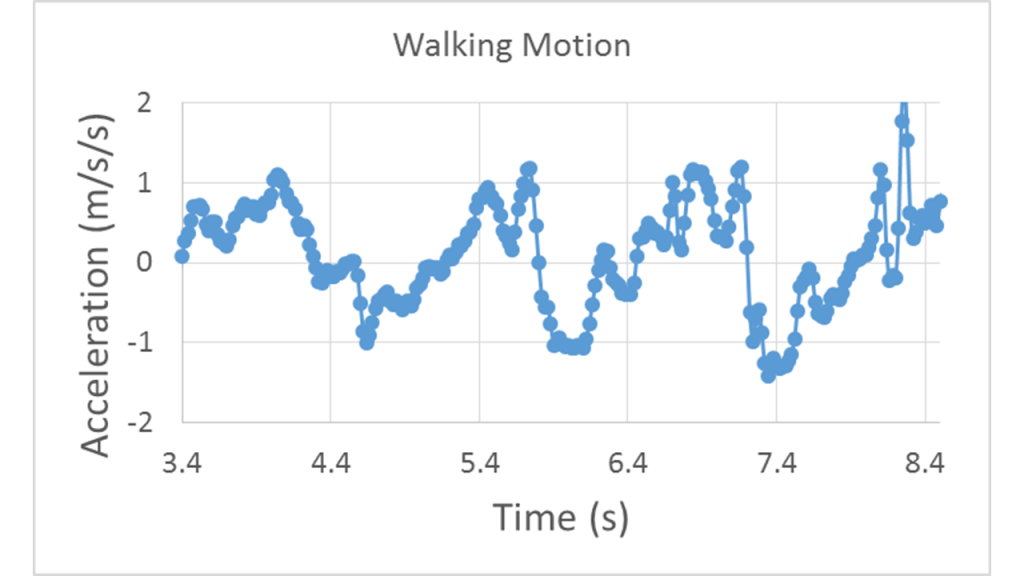
An initial positive acceleration corresponds with the change in velocity away from zero during the first step. Afterward, constant walking motion results in acceleration that oscillates from positive to negative and averages out to zero.

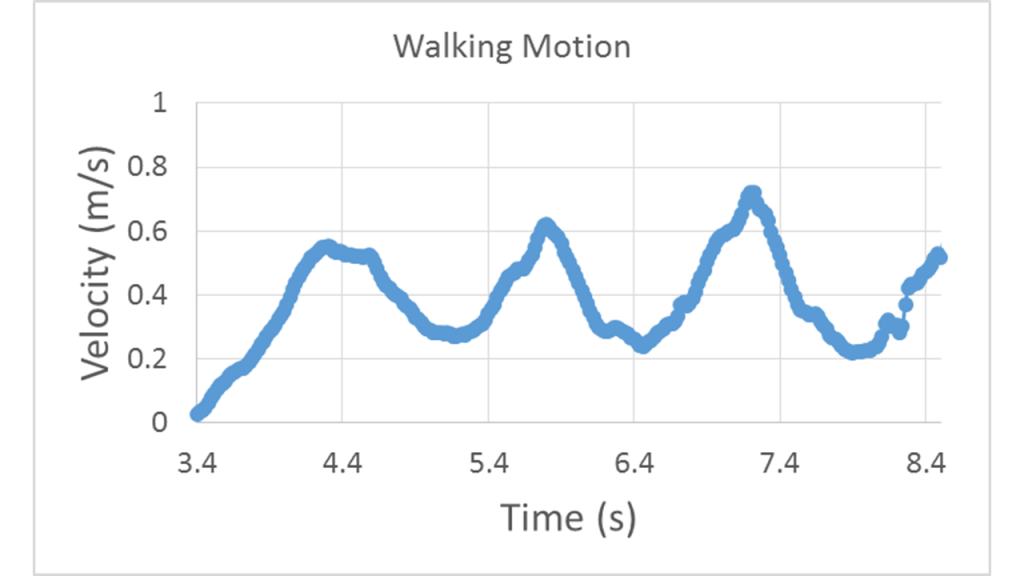
The oscillating accelerations result in a velocity that alternates between slowing down and speeding up, however we can see that the velocity stays positive so you are always making progress in the direction you intend to walk. We also see that over a full gait cycle average velocity is constant, near 0.4 m/s for this example, which agrees with the zero average acceleration in the previous graph.

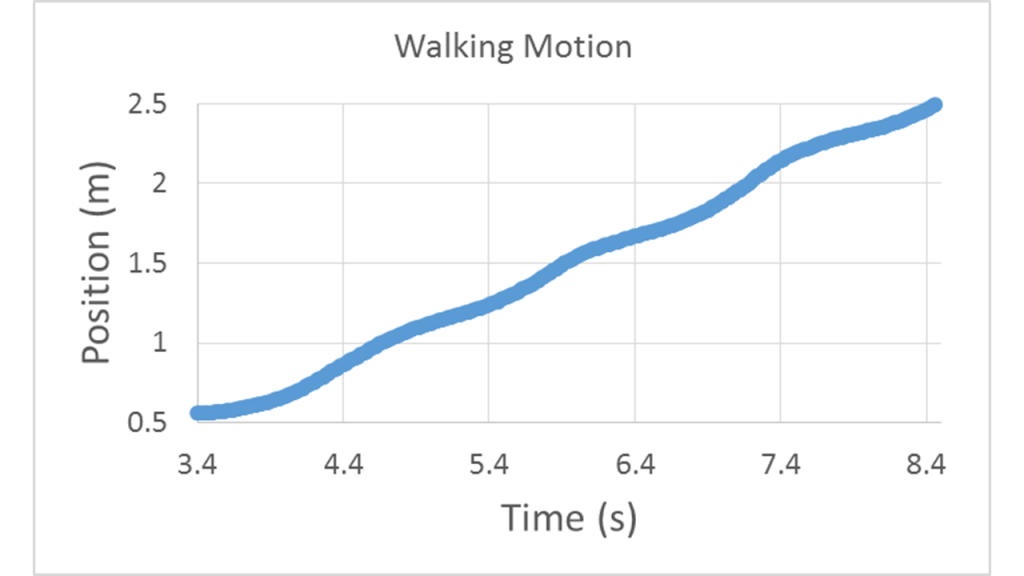
As you make progress, the position increases roughly linearly with an average slope equal to your constant average velocity, in this case 0.4 m/s. However the oscillations in the instantaneous velocity are noticeable as slight variations in the slope of the position graph.