Stress vs. Strain Curves

If you apply some stress to a material and measure the resulting strain, or vice versa, you can create a stress vs. strain curve like the one shown below for a typical metal.

^[1]

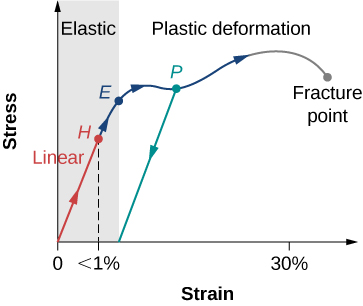
We see that the metal starts off with stress being proportional to strain, which means that the material is operating in its linear region. We have graphed stress on the vertical axis and strain on the horizontal axis, so the value of stress/strain is equal to the rise/run of the graph. We saw in the previous chapter that within the linear region stress/strain is equal to the the elastic modulus and we know the rise/run of a graph is the slope, therefore the elastic modulus of a material is equal to the slope of the linear portion its stress vs. curve. Let’s discuss the important features of the stress vs. strain curve:

1. The absolute highest point on the graph is the ultimate strength, indicating the onset of failure toward fracture or rupture.
2. Notice that after reaching the ultimate strength, but before full failure, the stress can actually decrease as strain increases, this is because the material is changing shape by breaking rather than stretching or compressing the distance between molecules in the material.
3. In the first part of the elastic region, the strain is proportional to the stress, this is known as the linear region. The slope of this region is the elastic modulus.
4. After the stress reaches the linearity limit (H) the slope is no longer constant, but the material still behaves elastically.
5. The elastic region ends and the plastic region begins at the yield point (E). In the plastic region, a little more stress causes a lot more strain because the material is changing shape at the molecular level. In some cases  the stress can actually decrease as strain increases,  because the material is changing shape by re-configuring molecules rather than just stretching or compressing the distance between molecules.
6. The green line originating at P illustrates the metal’s return to non-zero strain value  when the stress is removed after being stressed into the plastic region (permanent deformation).

Stress and Strain in Tendons

Tendons (attaching muscle to bone) and ligaments (attaching bone to bone) have somewhat unique behavior under stress.  Functionally, tendons and ligaments  must stretch easily at first to allow for flexibility, corresponding to the toe region of the stress-train curve shown below, but then resist significant stretching under large stress to prevent hyper-extension and dislocation injuries, corresponding to the linear region.

^[2]

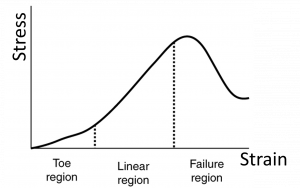
The structure of the tendon creates this specialized behavior. To create the toe region, a small stress causes the fibers in the tendon begin to align in the direction of the stress, or uncrimp, and the re-alignment provides additional length. Then in the linear region, the fibrils themselves will be stretched.

Stress and Strain Injuries

Stress beyond the yield point of a material will cause permanent deformation and the region of the stress vs. strain curve beyond the yield point is called the failure region. Stress above the ultimate strength will cause fracture or rupture.  These occurrences in body tissues are known as injuries. For example, sprains occur when a ligament (connects bone to bone) is torn by a stress greater than its ultimate strength or just stretched into its failure region. The same event occurring in a tendon (connects muscle to bone) is called known as strain.^[3] We already know that strain has a different, but related meaning to physicists and engineers, so that discrepancy in terminology is something to watch out for.