61 Physical Model for Terminal Velocity

After jumping, a skydiver begins gaining speed which increases the air resistance they experience. Eventually they will move fast enough that the air resistance is equal in size to their weight, but in opposite direction so they have no net force. This processes is illustrated by free body diagrams for a skydiver with 90 kg mass in the following image:

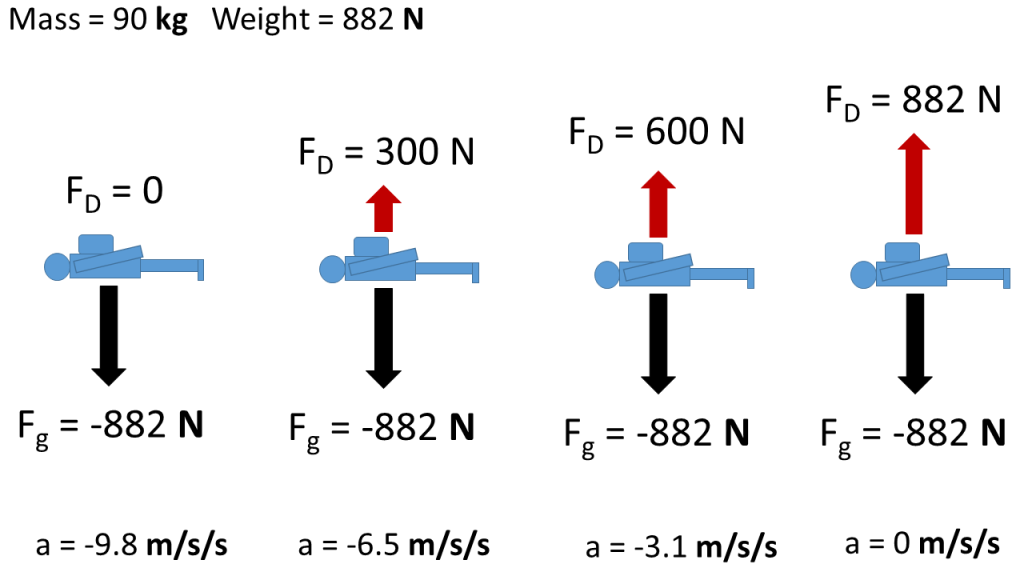
Free body diagrams showing the vertical forces of drag and gravity and resulting acceleration on a person at four times during a skydive from initial drop to terminal velocity. For all times the force of gravity is -888 N. The other example values are drag = zero, acceleration = -9.8 m/s/s; drag = 300 N, acceleration = -6.5 m/s/s; drag = 600 N, acceleration = -3.1 m/s/s, drag = 882 N, acceleration = 0.
Free body diagrams of a person with 90 kg mass during a skydive. The initial speed is zero, so drag force is zero. As speed increases, the drag force grows, eventually cancelling out the person’s weight. At that point acceleration is zero and terminal velocity is reached.

Dynamic Equilibrium

With a net force of zero the skydiver must be in equilibrium, but they are not in static equilibrium because they are not static (motionless). Instead they are in dynamic equilibrium, which means that they are moving, but the motion isn’t changing because all the forces are still balanced (net force is zero). This concept is summarized by Newton's First Law, which tells us that  an object’s motion will not change unless it experiences a net force. Newton’s first law is sometimes called the Law of Inertia because inertia is the name given to an object’s tendency to resist changes in motion.  Newton's First Law applies to objects that are not moving and to objects that are already moving. Regarding the skydiver, we are applying Newton’s First Law to translational motion (back and forth, up and down), but it  also holds for the effect of net torques on changes in rotational motion.  Changes in motion are known as accelerations and we will learn more about how net forces cause translational accelerations in upcoming chapters.

Everyday Example: Head Injuries

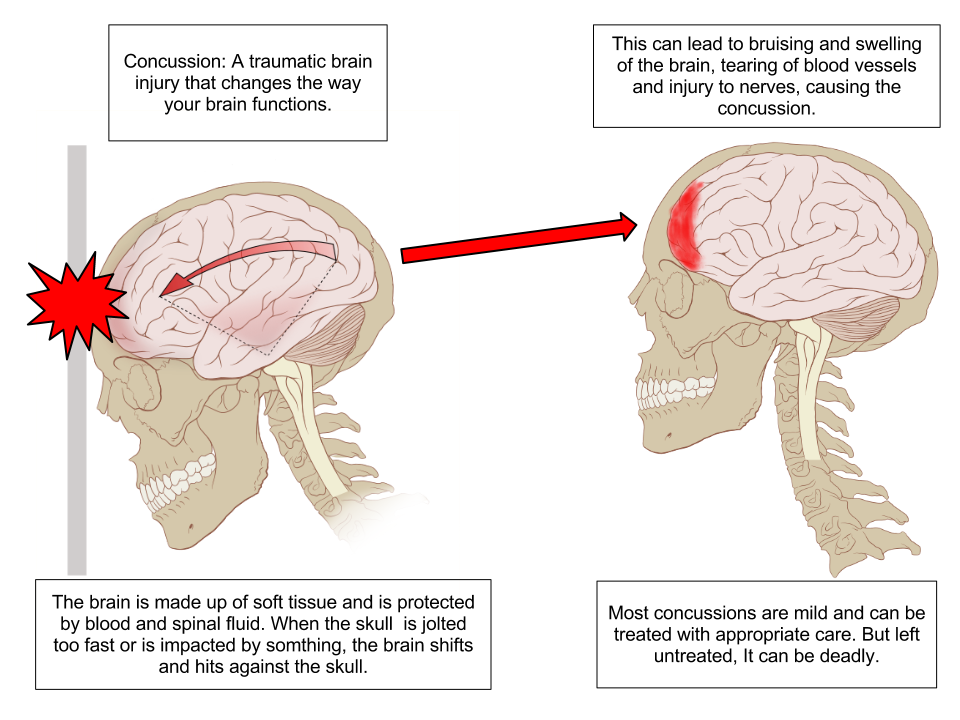First image: A human skull moving forward and stopping abruptly upon impact with a solid wall. A cutaway shows the brain continuing to move forward and impacting the front of the skull. Second image: The same skull with cutaway and injured area on the frontal lobe of the brain highlighted. Diagram of a concussion. “Concussion Anatomy” by Max Andrews via wikimedia commons.

[1]

When the head is travelling in a certain direction with constant speed the brain and skull are moving together. If an impact causes the the motion of the skull to change suddenly, the brain tends to continue its original motion according to Newton's First Law of Motion. The resulting impact between the fragile brain and the hard skull may result in a concussion. Recent research has shown that even without the occurrence of concussions, the damage caused by sub-concussive events like this can accumulate to cause Chronic Traumatic Encephalopathy (CTE)[2].

Reinforcement Exercises

Dependence of Terminal Velocity on Mass

We already know from our experimental work during the Unit 3 lab that increasing mass leads to increasing terminal speed. We can now understand that this behavior occurs because greater mass leads to a greater weight and thus a greater speed required before the drag force (air resistance) is large enough to balance out the weight and dynamic equilibrium is achieved.

Everyday Example: Tandem Skydive

First-time skydivers are typically attached to an instructor (tandem skydiving). During a tandem skydive the bodies are stacked, so the shape and cross-sectional area of the object don’t change much, but the mass does. As a consequence, the terminal speed for tandem diving would be high enough to noticeably reduce the fall time and possibly be dangerous. Increasing the air resistance to account for the extra mass is accomplished by deploying a small drag chute that trails behind the skydivers, as seen in the photo below.

Tandem skydivers with a small speed-limiting drag chute trailing behind. Image Credit: Fallschirm Tandemsprung bei Jochen Schweizer By Jochen Schweizer via Wikimedia Commons

[3]

A Physical Model for Terminal Velocity

When the skydiver has reached terminal speed and remains in a state of dynamic equilibrium, we know the size of the drag force must be equal to the skydiver’s weight, but in the opposite direction. This concept will allow us to determine how the skydiver’s mass should affect terminal speed. We start be equating the air resistance with the weight:

    \begin{equation*} F_d = F_g \end{equation*}

Then we insert the formulas for air resistance and for weight of an object near Earth’s surface. We designate the speed in the resulting equation v_T because these two forces are only equal at terminal speed.

    \begin{equation*} \frac{1}{2}C_d \rho A_x v_T^2 = mg \end{equation*}

We then need to solve the above equation for the terminal speed.

(1)   \begin{equation*} v_T = \sqrt{\frac{2mg}{C_d \rho A_x}} \end{equation*}

Everyday Examples: Terminal Speed of the Human Body

Let’s estimate the terminal speed of the human body. We start with the previous equation:

    \begin{equation*} v_T = \sqrt{\frac{2mg}{C_d \rho A_x}} \end{equation*}

We need to know the mass, drag coefficient, density of air, and cross-sectional area of the human body.  Let’s use the authors 80 kg mass and the density of air near the Earth’s surface at standard pressure and temperature, \rho = 1.2 \,\bold{kg/m^3}.  Drag coefficient and cross sectional area depend on body orientation, so let’s assume a standard skydiving posture: flat, horizontal, with arms and legs spread. In this case the drag coefficient will likely be 0.4-1.3.  A reasonable value would be C_d = 1[4]. To approximate the cross-sectional area we can use the authors average width of 0.3 m and height of 1.5 m  for an area of  A_x = 0.3 \bold{m} \times 1.5 {m} = 0.45 \,\bold{m^2}

Inserting these values into our terminal speed equation we have:

    \begin{equation*} v_T = \sqrt{\frac{2(80\,\bold{kg})(9.8\,\bold{m/s^2})}{1(1.2 \,\bold{kg/m^3}) (0.45\,\bold{m^2})}}= 54 \,\bold{m/s} = 120 \bold{MPH} \end{equation*}

Reinforcement Exercises

Acceleration During a Skydive

We have now analyzed the skydive after terminal speed was reached. Prior to this point the forces of drag and weight are not equal, therefore the skydiver is not in dynamic equilibrium and speed will change over time. In order to analyze the early part of the skydive we need to quantify changes motion and learn how those changes are related to the net force. The next chapters will help us with those two goals.

  1. Concussion Anatomy by Max Andrews - Own work. This file was derived from: Concussion mechanics.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=19490504 ↵
  2. "Concussion, microvascular injury, and early tauopathy in young athletes after impact head injury and an impact concussion mouse model" by Chad A Tagge, et. al, Brain, Oxford Academic ↵
  3. By Jochen Schweizer GmbH [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)], from Wikimedia Commons ↵
  4. "Drag Coefficient" by Engineering Toolbox ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Body Physics: Motion to Metabolism Copyright © by Lawrence Davis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book