40 Slipping

Slipping

Slipping happens when friction between feet and walking surface is not large enough to prevent your back foot from sliding as it pushes off, or the front foot from sliding when it tries to slow the forward motion of your center of gravity). Together, normal force and friction (F_f) provide the forces necessary to support the body and maintain balance. For example, friction prevents crutches from sliding outward when they aren’t held perfectly vertical. Friction is also necessary for locomotion, such as walking and running, as we will learn in the Locomotion unit.

Friction between the crutches and the floor prevents the young boy’s crutches from sliding outward even when they aren’t held straight vertical. This 1942 photo by Fritz Henle was captioned “Nurse training. Using the picture book as bait, the physical therapist encourages a young victim of infantile paralysis [Polio] to learn to use his catches (crutches).”  Polio was effectively eradicated from the United States by the polio vaccine, originally developed by Jonus Salk  “who never patented the vaccine or earned any money from his discovery, preferring it be distributed as widely as possible.” There are two types of vaccine that can prevent polio: inactivated poliovirus vaccine (IPV) and oral poliovirus vaccine (OPV). Only IPV has been used in the United States since 2000 and 99% of children who get all the recommended doses of vaccine will be protected from polio.

[1][2][3]

Friction

Friction (F_f) is the force that resists surfaces sliding against one another. Rub your palms together, the resistance you feel is friction. Complimentary to normal force, which only points perpendicular to surfaces, friction only points parallel to surfaces. Two surfaces must touch to have friction, so you also can’t get friction without normal force. In fact, frictional force is proportional to normal force.

Reinforcement Activity

Rub your palms together. Now push your palms together hard and try to slide them at the same time.

Now the normal force is larger causing the frictional force to grow in proportion.

The figure shows a crate on a flat surface, and a magnified view of a bottom corner of the crate and the supporting surface. The magnified view shows that there is roughness in the two surfaces in contact with each other. A black arrow points toward the right, away from the crate, and it is labeled as the direction of motion or attempted motion. A red arrow pointing toward the left is located near the bottom left corner of the crate, at the interface between that corner and the supporting surface. The red arrow is labeled as f, representing friction between the two surfaces in contact with each other.
Frictional forces always oppose sliding . Friction arises in part because of the roughness of the surfaces in contact, as seen in the expanded view. In order for the object to move, it must rise to where the peaks can skip along the bottom surface. Thus a force is required just to set the object in motion. Some of the peaks will be broken off, also requiring a force to maintain motion. Much of the friction is actually due to attractive forces between molecules making up the two objects, so that even smooth surfaces are not friction-free. The roughness and adhesion of the surfaces determine the coefficients of friction (μ).

 

Kinetic Friction

Kinetic friction (F_{f,k}) acts whenever two surfaces are sliding past one another and typically the size of the kinetic friction does not depend on the relative speed between the sliding surfaces. If an object is sliding, but there not another force pushing the object to keep it sliding, then kinetic friction will eventually stop the sliding object. (Give an object a shove so that it slides across the floor and it will eventually stop. That is kinetic friction at work).

Static Friction

Unlike kinetic friction, static friction does not have a constant value. Instead, static friction adjusts to prevent the surfaces from slipping, but it can only do so up to a maximum value. If the force required to prevent slipping is larger than the maximum static friction value, the object will slide and kinetic friction takes over. Static friction is larger than kinetic friction. The following graph of force vs. time demonstrates the process of “breaking free” of static friction between two surfaces. The graph was created by measuring the force that students applied to a box sitting on a table by pulling on a string tied to the box.

Pull force applied to a box on a table. The students pulled lightly at first, then increasingly harder until the box began to slide, and then pulled just right to keep the box moving at constant speed. Notice that as the students pull harder the box has not yet move, which means the static frictional responds and grows larger to prevent sliding from occurring. A maximum of static frictional force of 6.4 N is reached before the box begins to slide and kinetic friction takes over. We see that the force drops at this point, meaning that the students had to reduce their pull force to 5.5 N in order to just balance kinetic friction and maintain a constant speed. This demonstrates that kinetic friction is smaller than static friction. This data is was acquired by Umpqua Community College physics students Libby Fregoso and McKenzie Carrier.

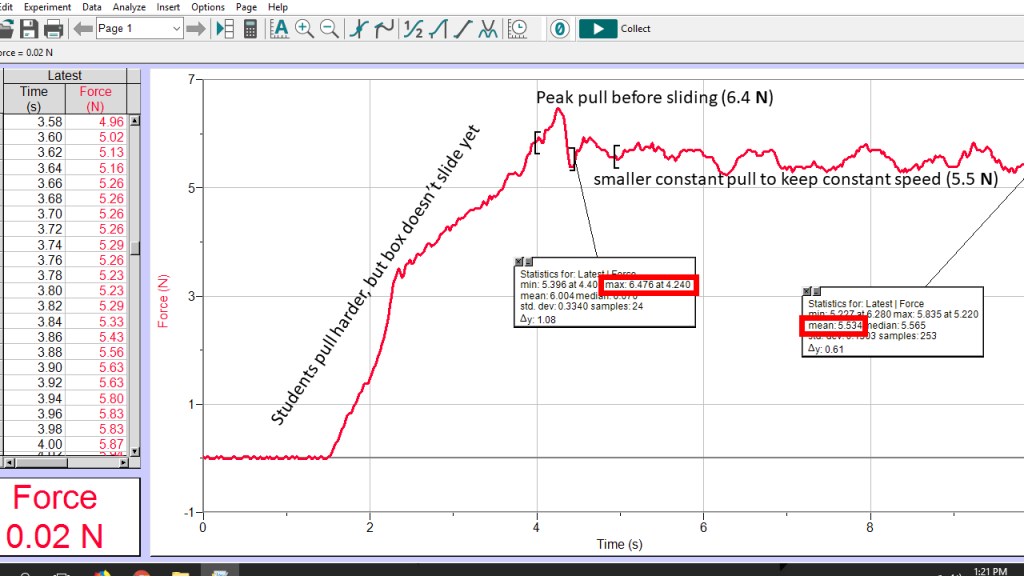
Choose the friction simulation from the simulation set to see how static and kinetic friction behave.

Reinforcement Activity

Friction Coefficient

We now know that friction force is proportional to normal force and that there are two types of friction, static and kinetic. The final concept that affects friction is the roughness, or alternatively the smoothness, of the two surfaces. The coefficient of friction (\mu) is a unitless number that rates the roughness and is typically determined experimentally. The static frictional force is larger than the kinetic frictional forces because \mu_s is larger than \mu_k. Take a look at the table of static and kinetic friction coefficients found below. You can find more values in this massive table of static friction coefficients.

Table of static and kinetic friction coefficients for various surface pairs[4]
\textbf{System} \textbf{Static friction,}\boldsymbol{\mu_{\textbf{s}}} \textbf{Kinetic friction,}\boldsymbol{\mu_{\textbf{k}}}
Rubber on dry concrete 1.0 0.7
Rubber on wet concrete 0.7 0.5
Wood on wood 0.5 0.3
Waxed wood on wet snow 0.14 0.1
Metal on wood 0.5 0.3
Steel on steel (dry) 0.6 0.3
Steel on steel (oiled) 0.05 0.03
Teflon on steel 0.04 0.04
Bone lubricated by synovial fluid 0.016 0.015
Shoes on wood 0.9 0.7
Shoes on ice 0.1 0.05
Ice on ice 0.1 0.03
Steel on ice 0.4 0.02

Notice that two surfaces are always listed in the table; you must have two surfaces to define a \mu.  When someone asks a question like, “what is the \mu of ice?” they usually mean between ice and ice, but its best to avoid asking such questions and just always reference two surfaces.

Calculating Friction Forces

We can sum up everything we have learned about friction in two equations that relate the friction forces to the friction coefficient for two surfaces and the normal force acting on the surfaces:

Max static friction before release:

(1)   \begin{equation*} F^{max}_{f,s} = \mu_{s}F_{N} \end{equation*}

Kinetic friction once moving:

(2)   \begin{equation*} F_{f,k} = \mu_{k}F_{N} \end{equation*}

Everyday Example: Firefighter Physical Ability Test

Firefighter candidates must complete a physical ability test (PAT) that includes dragging a dummy across the floor. The PAT for the city of Lincoln Nebraska specifies that candidates must drag a human form dummy weighing 170 lbs for 25 feet, around a barrel, and then back across the starting point for a total distance of 50 feet in six minutes or less. The candidates may only drag the dummy using the pull harness attached to the dummy and cannot carry the dummy[5].

The test is held on a polished concrete floor. The static friction coefficient between cotton clothing and polished concrete is 0.5. If a candidate pulls vertically up on the harness with a force of 70 lbs what horizontal pull force must the candidate apply in order to get the dummy moving?

The dummy starts out in static equilibrium so we know the net force must be zero in both the veritical and horizontal directions. First, let’s analyze the vertical direction: if the candidate pulls vertically up on the harness with a force of 70 lbs then the floor must provide a normal force of 100 lbs  to support the dummy.

Now let’s analyze the horizontal direction: static friction will match whatever horizontal pull the candidate provides, but in the opposite direction, so that the dummy stays in static equilibrium until the pull exceeds the max static friction force. That’s the force the candidate needs to apply to get the dummy moving, so let’s find that. We have the friction coefficient and we already found the normal force so we are ready:

    \begin{equation*} F^{max}_{f,s} = \mu_sF_N =0.5\cdot100\, \bold{lbs} = 50\, \bold{lbs} \end{equation*}

After the dummy starts moving, kinetic friction kicks in so we can use \mu_k = 0.4 to calculate the kinetic frictional force. The is force is less than the max static frictional force, so it will require less force to keep the dummy moving than it did to get it started.

    \begin{equation*} F_{f,k} = \mu_kF_N =0.4\cdot100\, \bold{lbs} = 40\, \bold{lbs} \end{equation*}

Reinforcement Exercises

A person clings to a playground fire pole. “Firepole” by Donkeysforever, via Wikimedia Commons is in the Public domain

 

The equations given for static and kinetic friction are empirical models that describe the behavior of the forces of friction. While these formulas are very useful for practical purposes, they do not have the status of laws or principles. In fact, there are cases for which these equations are not even good approximations. For instance, neither formula is accurate for surfaces that are well lubricated or sliding at high speeds. Unless specified, we will not be concerned with these exceptions.[6]

  1. "Photo" by Fritz Henle, Library of Congress is in the Public Domain ↵
  2. "History of Salk" by The Salk Institute ↵
  3. "What is Polio" by Global Heatlh, Center for Disease Control ↵
  4. OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Aug 2, 2018 http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@11.1. ↵
  5. "Firefighter Physical Ability Test Candidate Orientation Guide" by Industrial/Organizational Solutions, Inc. ↵
  6. OpenStax University Physics, University Physics Volume 1. OpenStax CNX. Aug 2, 2018 http://cnx.org/contents/d50f6e32-0fda-46ef-a362-9bd36ca7c97d@11.1. ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Body Physics: Motion to Metabolism Copyright © by Lawrence Davis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book