26 Unit 3 Practice and Assessment

Outcomes 1, 2, 3 

  1. Would putting larger tires on a vehicle introduce random or systematic error into the speedometer reading? Would this affect the accuracy or precision (or both) of the speedometer? Explain your answers.

 

  1. Would a wiggling baby introduce random or systematic error into a measurement of its weight? Would this affect the accuracy or precision (or both) of the weight measurement? Explain your answers.

 

  1. Would slightly under-filling measuring cups to prevent spilling ingredients introduce random or systematic error into the measurement of ingredient volumes? Would this affect the accuracy or precision (or both) of the measurement volumes. Explain your answers.

A set of measurements of a physical quantity was made for comparison to an accepted standard value. The data were plotted in graphs with the measured values on the horizontal axis and the number of times each value occurred on the vertical axis. This type of graph is known as a histogram and the data on the vertical axis are called the frequencies. Use the histograms below to answer the questions that follow.

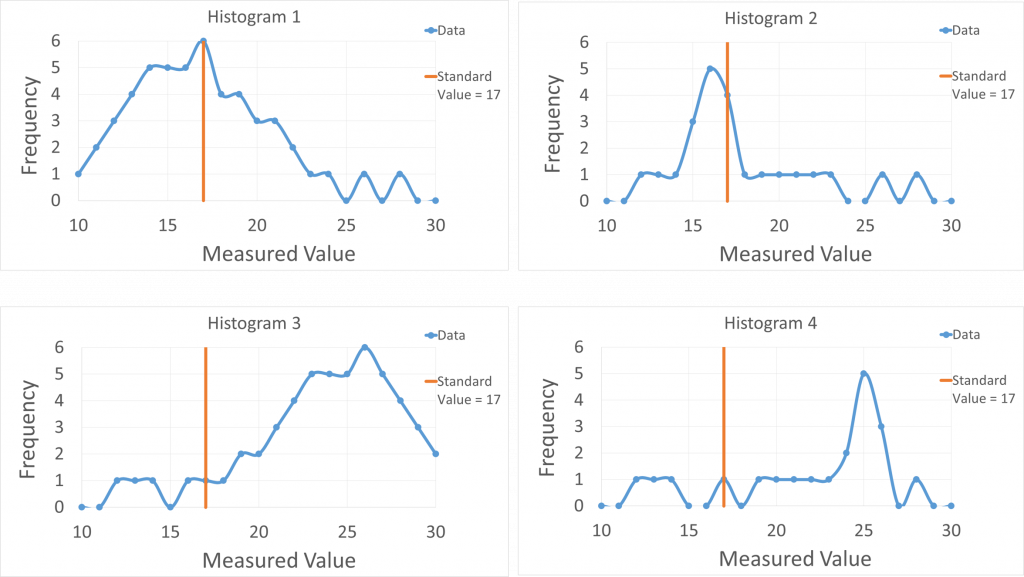
Each histogram has measurement value plotted on the horizontal axis and frequency of occurrence for each value on the vertical axis. Each histogram has a vertical line crossing measurement value 17 to indicate the accepted standard value of this measurement. Histogram 1 has peak frequency of 6 near value 17 and frequencies greater than 2 between values 12 and 22. Histogram 2 has a maximum near a value of 16 and no frequency greater than 2 outside the range of values 15 to 18. Histogram 3 has a maximum near 26 and frequencies greater than two between value 22 and 30. Histogram 4 has a maximum near a value of 25 and has frequency greater than 2 between values 24 and 26.
Histograms of values measured during an experiment.
  1. For each histogram state whether the data suggest the measurements were relatively accurate, precise, both, or neither. Explain your reasoning.
  2. For each histogram state what types of errors were likely to be relatively significant: random, systematic, both or neither. Explain your reasoning.

    Outcome 4

    6)A person measures his or her heart rate by counting the number of beats in 30 s as timed using a clock on the wall, such as the one in the image below. They start counting when the second hand jumps onto a particular tick mark (say the 12) and then stop counting when it jumps to the opposite mark (say the 6). A reasonable estimate of the uncertainty in the time measurement would be which of the values listed below? Explain your reasoning.

a) 0.05 s

b) 0.5 s

c) 5 s

d) 50 s

 

Typical wall clock with hour, minute, second hands and 1 hour, 1 min (1s) divisions. Image Credit: Clock by Lee Haywood via Wikimedia Commons

[1]

  1. Estimate the uncertainty in counting the beats in the previous problem. Explain your reasoning.

*8) If 47 beats were counted by the person in the previous problem, what a was their heart rate in BPM in correct significant figures. Indicate the total % uncertainty and total uncertainty.

  1. Clock By Lee Haywood from Wollaton, Nottingham, England (Clock) [CC BY-SA 2.0 (https://creativecommons.org/licenses/by-sa/2.0)], via Wikimedia Commons ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Body Physics: Motion to Metabolism Copyright © by Lawrence Davis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book